2 День 1. Основы R
2.1 Знакомимся с самым базовым
2.1.1 Установка R и Rstudio
Для работы с R необходимо его сначала скачать и установить.
- R
- на Windows, найдите большую кнопку Download R (номер версии) for Windows.
- на Mac, если маку меньше, чем 5 лет, то смело ставьте *.pkg файл с последней версией. Если старше, то поищите на той же странице версию для вашей системы.
- на Linux, также можно добавить зеркало и установить из командной строки:
sudo apt-get install r-cran-baseВ данной книге используется следующая версия R:
sessionInfo()$R.version$version.string## [1] "R version 3.6.0 (2019-04-26)"После установки R необходимо скачать и установить RStudio:
Если вдруг что-то установить не получается (или же вы просто не хотите устанавливать на компьютер лишние программы), то можно работать в облаке, делая все то же самое в веб-браузере:
Первый и вполне закономерный вопрос: зачем мы ставили R и отдельно еще какой-то RStudio? Если опустить незначительные детали, то R — это сам язык программирования, а RStudio — это среда (IDE), которая позволяет в этом языке очень удобно работать.
RStudio — это единственная среда для R, но, определенно, самая удобная на сегодняшний день, у нее практически нет конкурентов. Почти все пользуются именно ею и не стоит тратить время на поиск чего-то более удобного и лучшего. Если же вы привыкли работать с Jupyter Notebook
Естественно, RStudio — не единственная среда для R, но, определенно, самая крутая. Почти все пользуются именно ею и не стоит тратить время на поиск чего-то более удобного и лучшего. Если Вы привыкли к Jupyter Notebook, то здесь тоже есть ноутбуки (RNotebook — хотя это и не совсем то же самое), но еще есть и кое-что покруче — RMarkdown. И с этим мы тоже разберемся!
2.1.2 RStudio
Так, давайте взглянем на то, что нам тут открылось:
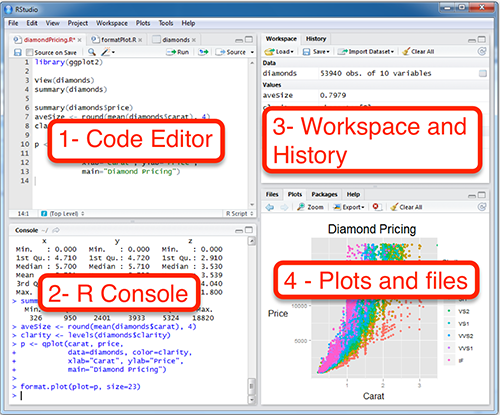
В первую очередь нас интересуют два окна: 1 - Code Editor (окно для написания скриптов)1 и 2 - R Console (консоль). Здесь можно писать команды и запускать их. При этом работа в консоли и работа со скриптом немного различается.
В 2 - R Console вы пишите команду и запускаете ее нажиманием Enter. Иногда после запуска команды появляется какой-то результат. Если нажимать стрелку вверх на клавиатуре, то можно выводить в консоль предыдущие команды. Это очень удобно для запуска предыдущих команд с небольшими изменениями.
В 1 - Code Editor для запуска команды вы должны выделить ее и нажать Ctrl + Enter (Cmd + Enter на macOS). Если не нажать эту комбинацию клавиш, то команда не запустится. Можно выделить и запустить сразу несколько команд или даже все команды скрипта. Все команды скрипта можно выделить с помощью сочетания клавиш Ctrl + A на Windows и Linux, Cmd + A на macOS.2 Как только вы запустите команду (или несколько команд), соответствующие строчки кода появятся в 2 - R Console, как будто бы вы запускали их прямо там.
Обычно в консоли удобно что-то писать, чтобы быстро что-то посчитать. Скрипты удобнее при работе с длинными командами и как способ сохранения написанного кода для дальнейшей работы. Для сохранения скрипта нажмите File - Save As.... R скрипты сохраняются с разрешением .R, но по своей сути это просто текстовые файлы, которые можно открыть и модифицировать в любом текстовом редакторе а-ля “Блокнот”.
3 - Workspace and History — здесь можно увидеть переменные. Это поле будет автоматически обновляться по мере того, как Вы будете запускать строчки кода и создавать новые переменные. Еще там есть вкладка с историей всех команд, которые были запущены.
4 - Plots and files. Здесь есть очень много всего. Во-первых, небольшой файловый менеджер, во-вторых, там будут появляться графики, когда вы будете их рисовать. Там же есть вкладка с вашими пакетами (Packages) и Help по функциям. Но об этом потом.
2.1.3 R как калькулятор
R — полноценный язык программирования, который позволяет решать широкий спектр задач. Но в первую очередь R используется для анализа данных и статистических вычислений. Тем не менее, многими R до сих пор воспринимается как просто продвинутый калькулятор. Ну что ж, калькулятор, так калькулятор.
Давайте начнем с самого простого и попробуем использовать R как калькулятор с помощью арифметических операторов +, -, *, /, ^ (степень), () и т.д.
Просто запускайте в консоли пока не надоест:
40+2## [1] 423-2## [1] 15*6## [1] 3099/9 #деление## [1] 112^3 #степень## [1] 813 %/% 3 #целочисленное деление## [1] 413 %% 3 #остаток от деления## [1] 1Попробуйте самостоятельно посчитать что-нибудь с разными числами.

Ничего сложного, верно? Вводим выражение и получаем результат.
Вы могли заметить, что некоторые команды у меня заканчиваются знаком решетки (#). Все, что написано в строчке после # игнорируется R при выполнении команды. Написанные команды в скрипте рекомендуется сопровождать комментариями, которые будут объяснять вам же в будущем (или кому-то еще), что конкретно происходит в соответствующем куске кода.3 Кроме того, комментарии можно использовать в тех случаях, когда вы хотите написать кусок кода по-другому, не стирая полностью предыдущий код: достаточно “закомментить” нужные строчки - поставить # в начало каждой строки, которую вы хотите переписать. Для этого есть специальное сочетание горячих клавиш: Ctrl + Shift + C (Cmd + Shift + C на macOS) — во всех выделенных строчках будет написан # в начале.
Согласно данным навязчивых рекламных баннеров в интернете, только 14% россиян могут справиться с этим примером:
2 + 2 * 2## [1] 6На самом деле, разные языки программирования ведут себя по-разному в таких ситуациях, поэтому ответ 6 (сначала умножаем, потом складываем) не так очевиден.
Порядок выполнения арифметических операций (т.е. приоритет операторов, operator precedence) в R как в математике, так что не забывайте про скобочки.
(2+2)*2## [1] 8Если Вы не уверены в том, какие операторы имеют приоритет, то используйте скобочки, чтобы точно обозначить, в каком порядке нужно производить операции. Или же смотрите на таблицу приоритета операторов с помощью команды ?Syntax.
2.1.4 Функции
Давайте теперь извлечем корень из какого-нибудь числа. В принципе, тем, кто помнит школьный курс математики, возведения в степень вполне достаточно:
16^0.5## [1] 4Ну а если нет, то можете воспользоваться специальной функцией: это обычно какие-то буквенные символы с круглыми скобками сразу после названия функции. Мы подаем на вход (внутрь скобочек) какие-то данные, внутри этих функций происходят какие-то вычисления, которые выдает в ответ какие-то другие данные (или же функция записывает файл, рисует график и т.д.).
Вот, например, функция для корня:
sqrt(16)## [1] 4R — case-sensitive язык, т.е. регистр важен. SQRT(16) не будет работать.
А вот так выглядит функция логарифма:
log(8)## [1] 2.079442Так, вроде бы все нормально, но… Если Вы еще что-то помните из школьной математики, то должны понимать, что что-то здесь не так.
Здесь не хватает основания логарифма!
Логарифм — показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.
То есть у логарифма 8 по основанию 2 будет значение 3:
\(\log_2 8 = 3\)
То есть если возвести 2 в степень 3 у нас будет 8:
\(2^3 = 8\)
Только наша функция считает все как-то не так.
Чтобы понять, что происходит, нам нужно залезть в хэлп этой функции:
?logСправа внизу в RStudio появится вот такое окно:
Действительно, у этой функции есть еще аргумент base =. По дефолту он равен числу Эйлера (2.7182818…), т.е. функция считает натуральный логарифм. В большинстве функций R есть какой-то основной инпут — данные в том или ином формате, а есть и дополнительные параметры, которые можно прописывать вручную, если параметры по умолчанию нас не устраивают.
log(x = 8, base = 2)## [1] 3…или просто (если Вы уверены в порядке переменных):
log(8,2)## [1] 3Более того, Вы можете использовать оутпут одних функций как инпут для других:
log(8, sqrt(4))## [1] 3Отличненько. Мы еще много раз будем возвращаться к функциям. Вообще, функции — это одна из важнейших штук в R (примерно так же как и в Python). Мы будем создавать свои функции, использовать функции как инпут для функций и многое-многое другое. В R очень крутые возможности работы с функциями. Поэтому подружитесь с функциями, они клевые.
Арифметические знаки, которые мы использовали:
+,-,/,^и т.д. называются операторами и на самом деле тоже являются функциями:
'+'(3, 4)## [1] 72.1.5 Переменные
Важная штука в программировании на практически любом языке — возможность сохранять значения в переменных. В R это обычно делается с помощью вот этих символов: <- (но можно использовать и обычное =, хотя это не очень принято). Для этого есть удобное сочетание клавиш: нажмите одновременно Alt + - (или option + - на macOS).
a <- 2
a## [1] 2Заметьте, при присвоении результат вычисления не выводится в консоль! Если опустить детали, то обычно результат выполнения комманды либо выводится в консоль, либо записывается в переменную.
После присвоения переменная появляется во вкладке Environment в RStudio:
Можно использовать переменные в функциях и просто вычислениях:
b <- a ^ a + a * a
b## [1] 8log(b, a)## [1] 3Вы можете сравнивать разные переменные:
a == b## [1] FALSEЗаметьте, что сравнивая две переменные мы используем два знака равно ==, а не один =. Иначе это будет означать присвоение.
a = b
a## [1] 8Теперь Вы сможете понять комикс про восстание роботов на следующей странице (пусть он и совсем про другой язык программирования)

Этот комикс объясняет, как важно не путать присваивание и сравнение (хотя я иногда путаю до сих пор =( ).
Иногда нам нужно проверить на неравенство:
a <- 2
b <- 3
a==b## [1] FALSEa!=b## [1] TRUEВосклицательный язык в программировании вообще и в R в частности стандартно означает отрицание.
Еще мы можем сравнивать на больше/меньше:
a > b## [1] FALSEa < b## [1] TRUEa >= b## [1] FALSEa <= b## [1] TRUE2.2 Типы данных
До этого момента мы работали только с числами (numeric):
class(a)## [1] "numeric"Вообще, в R много типов numeric: integer (целые), double (с десятичной дробью), complex (комплексные числа). Последние пишутся так:
complexnumber <- 2+2iОднако в R с этим обычно можно вообще не заморачиваться, R сам будет конвертить между форматами при необходимости. Немного подробностей здесь:
Разница между numeric и integer, Как работать с комплексными числами в R
Теперь же нам нужно ознакомиться с двумя другими важными типами данных в R:
- character: строки символов. Они должны выделяться кавычками. Можно использовать как
", так и'(что удобно, когда строчка внутри уже содержит какие-то кавычки).
s <- "Всем привет!"
s## [1] "Всем привет!"class(s)## [1] "character"- logical: просто
TRUEилиFALSE.
t1 <- TRUE
f1 <- FALSE
t1## [1] TRUEf1## [1] FALSEВообще, можно еще писать T и F (но не True и False!)
t2 <- T
f2 <- FЭто дурная практика, так как R защищает от перезаписи переменные TRUE и FALSE, но не защищает от этого T и F
TRUE <- FALSE## Error in TRUE <- FALSE: неправильная (do_set) левая сторона в присвоенииTRUE## [1] TRUET <- FALSE
T## [1] FALSEТеперь вы можете догадаться, что результаты сравнения, например, числовых или строковых переменных вы можете сохранять в переменные тоже!
comparison <- a == b
comparison## [1] FALSEЭто нам очень понадобится, когда мы будем работать с реальными данными: нам нужно будет постоянно вытаскивать какие-то данные из датасета, а это как раз и построено на игре со сравнением переменных.
Чтобы этим хорошо уметь пользоваться, нам нужно еще освоить как работать с логическими операторами. Про один мы немного уже говорили — это не (!):
t1## [1] TRUE!t1## [1] FALSE!!t1 #Двойное отрицание!## [1] TRUEЕще есть И (выдаст TRUE только в том случае если обе переменные TRUE):
t1 & t2## [1] TRUEt1 & f1## [1] FALSEА еще ИЛИ (выдаст TRUE в случае если хотя бы одна из переменных TRUE):
t1 | f1## [1] TRUEf1 | f2## [1] FALSEПоздравляю, мы только что разобрались с самой занудной (но очень важной!) частью. Пора переходить к важному и интересному. ВЕКТОРАМ!
2.3 Вектор
Если у вас не было линейной алгебры (или у вас с ней было все плохо), то просто запомните, что вектор (atomic vector или просто atomic) — это набор (столбик) чисел в определенном порядке.
Если вы привыкли из школьного курса физики считать вектора стрелочками, то не спешите возмущаться и паниковать. Представьте стрелочки как точки из нуля координат {0,0} до какой-то точки на координатной плоскости, например, {2,3}:
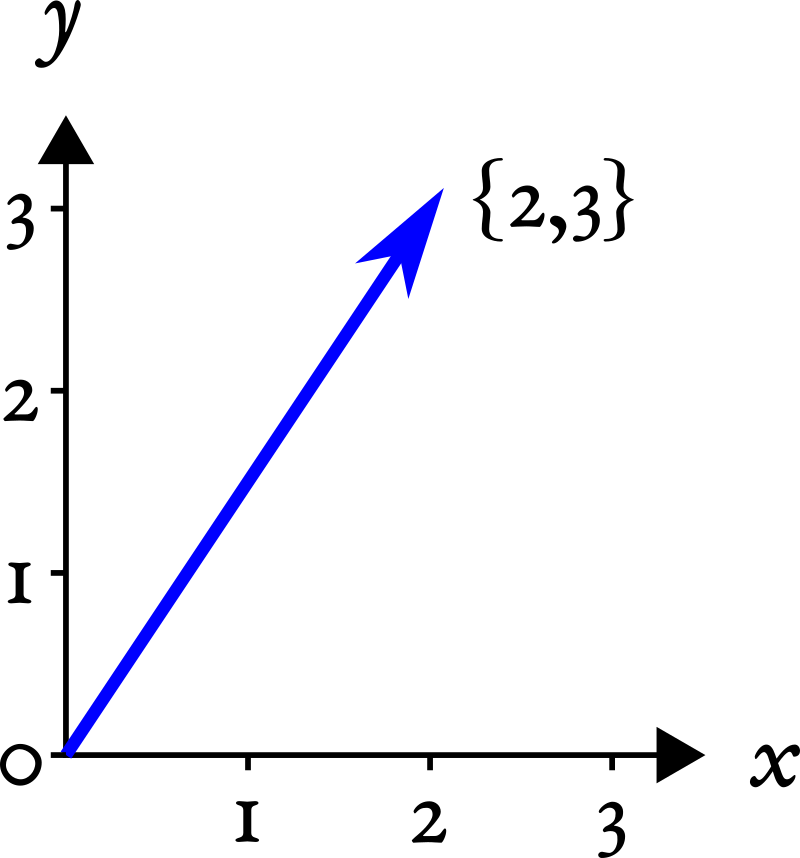
Вот последние два числа и будем считать вектором. Попытайтесь теперь мысленно стереть координатную плоскость и выбросить стрелочки из головы, оставив только последовательность чисел {2,3}:

На самом деле, мы уже работали с векторами в R, но, возможно, вы об этом даже не догадывались. Дело в том, что в R нет как таковых скалярных (т.е. одиночных) значений, есть вектора длиной 1. Такие дела!
Чтобы создать вектор из нескольких значений, нужно воспользоваться функцией c():
c(4,8,15,16,23,42)## [1] 4 8 15 16 23 42Создавать вектора можно не только из numeric, но также и из character и logical:
c("Хэй", "Хэй", "Ха")## [1] "Хэй" "Хэй" "Ха"c(TRUE, FALSE)## [1] TRUE FALSEОдна из самых мерзких и раздражающих причин ошибок в коде — это использование
сиз кириллицы вместоcиз латиницы. Видите разницу? И я не вижу. А R видит.
Для создания числовых векторов есть удобный оператор :
1:10## [1] 1 2 3 4 5 6 7 8 9 105:-3## [1] 5 4 3 2 1 0 -1 -2 -3Этот оператор создает вектор от первого числа до второго с шагом 1. Вы не представляете, как часто эта штука нам пригодится… Если же нужно сделать вектор с другим шагом, то есть функция seq():
seq(10,100, by = 10)## [1] 10 20 30 40 50 60 70 80 90 100Кроме того, можно задавать не шаг, а длину вектора. Тогда шаг функция seq() посчитает сама:
seq(1,13, length.out = 4)## [1] 1 5 9 13Другая функция — rep() — позволяет создавать вектора с повторяющимися значениями. Первый аргумент — значение, которое нужно повторять, а второй аргумент — сколько раз повторять.
rep(1, 5)## [1] 1 1 1 1 1И первый, и второй аргумент могут быть векторами!
rep(1:3, 3)## [1] 1 2 3 1 2 3 1 2 3rep(1:3, 1:3)## [1] 1 2 2 3 3 3Еще можно объединять вектора (что мы, по сути, и делали, просто с векторами длиной 1):
v1 <- c("Hey", "Ho")
v2 <- c("Let's", "Go!")
c(v1, v2)## [1] "Hey" "Ho" "Let's" "Go!"Очень многие функции в R работают именно с векторами. Например, функции sum() (считает сумму значений вектора) и mean() (считает среднее арифметическое всех значений в векторе):
sum(1:10)## [1] 55mean(1:10)## [1] 5.52.3.1 Приведение типов
Что будет, если вы объедините два вектора с значениями разных типов? Ошибка?
Мы уже обсуждали, что в atomic может быть только один тип данных. В некоторых языках программирования при операции с данными разных типов мы бы получили ошибку. А вот в R при несовпадении типов пройзойдет попытка привести типы к “общему знаменателю”, то есть конвертировать данные в более “широкий” тип.
Например:
c(FALSE, 2)## [1] 0 2FALSE превратился в 0 (а TRUE превратился бы в 1), чтобы оба значения можно было объединить в вектор. То же самое произошло бы в случае операций с векторами:
2 + TRUE## [1] 3Это называется неявным приведением типов (implicit coercion).
Вот более сложный пример:
c(TRUE, 3, "Привет")## [1] "TRUE" "3" "Привет"У R есть иерархия коэрсинга:
NULL < raw < logical < integer < double < complex < character < list < expression.
Мы из этого списка еще многого не знаем, сейчас важно запомнить, что логические данные — TRUE и FALSE — превращаются в 0 и 1 соответственно, а 0 и 1 в строчки "0" и "1".
Если Вы боитесь полагаться на приведение типов, то можете воспользоваться функциями as.нужныйтипданных для явного приведения типов (explicit coercion):
as.numeric(c(T, F, F))## [1] 1 0 0as.character(as.numeric(c(T, F, F)))## [1] "1" "0" "0"Можно превращать и обратно, например, строковые значения в числовые. Если среди числа встретится буква или другой неподходящий знак, то мы получим предупреждение NA — пропущенное значение (мы очень скоро научимся с ними работать).
as.numeric(c("1", "2", "три"))## Warning: в результате преобразования созданы NA## [1] 1 2 NAОдин из распространенных примеров использования неявного приведения типов — использования функций
sum()иmean()для подсчета в логическом векторе количества и долиTRUEсоответсвенно. Мы будем много раз пользоваться этим приемом в дальнейшем!
2.3.2 Векторизация
Все те арифметические операторы, что мы использовали ранее, можно использовать с векторами одинаковой длины:
n <- 1:4
m <- 4:1
n + m## [1] 5 5 5 5n - m## [1] -3 -1 1 3n * m## [1] 4 6 6 4n / m## [1] 0.2500000 0.6666667 1.5000000 4.0000000n ^ m + m * (n - m)## [1] -11 5 11 7Если применить операторы на двух векторах одинаковой длины, то в мы получим результат поэлементного применения оператора к двум векторам. Это называется векторизацией (vectorization).
Если после какого-нибудь MATLAB Вы привыкли, что по умолчанию операторы работают по правилам линейной алгебры и
m*nбудет давать скалярное произведение (dot product), то снова нет. Для скалярного произведения нужно использовать операторы с%по краям:
n %*% m## [,1]
## [1,] 20Абсолютно так же и с операциями с матрицами в R, хотя про матрицы будет немного позже.
В принципе, большинство функций в R, которые работают с отдельными значениями, так же хорошо работают и с целыми векторами. Скажем, Вы хотите извлечь корень из нескольких чисел, для этого не нужны никакие циклы (как это обычно делается в других языках программирования). Можно просто “скормить” вектор функции и получить результат применения функции к каждому элементу вектора:
sqrt(1:10)## [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751
## [8] 2.828427 3.000000 3.162278Таких векторизованных функций в R очень много. Многие из них написаны на более низкоуровневых языках программирования (C, C++, FORTRAN), за счет чего использование таких функций приводит не только к более элегантному, лаконичному, но и к более быстрому коду.
Векторизация в R — это очень важная фишка, которая отличает этот язык программирования от многих других. Если вы уже имеете опыт программирования на другом языке, то вам во многих задачах захочется использовать циклы типа
forиwhile3.2.3. Не спешите этого делать! В очень многих случаях циклы можно заменить векторизацией. Тем не менее, векторизация — это не единственный способ избавить от циклов типаforиwhile3.2.5.
2.3.3 Recycling
Допустим мы хотим совершить какую-нибудь операцию с двумя векторами. Как мы убедились, с этим обычно нет никаких проблем, если они совпадают по длине. А что если вектора не совпадают по длине? Ничего страшного! Здесь будет работать правило ресайклинга (правило переписывания, recycling rule). Это означает, что если мы делаем операцию на двух векторах разной длины, то если короткий вектор кратен по длине длинному, короткий вектор будет повторяться необходимое количество раз:
n <- 1:4
m <- 1:2
n * m## [1] 1 4 3 8А что будет, если совершать операции с вектором и отдельным значением? Можно считать это частным случаем ресайклинга: короткий вектор длиной 1 будет повторятся столько раз, сколько нужно, чтобы он совпадал по длине с длинным:
n * 2## [1] 2 4 6 8Если же меньший вектор не кратен большему (например, один из них длиной 3, а другой длиной 4), то R посчитает результат, но выдаст предупреждение.
n + c(3,4,5)## Warning in n + c(3, 4, 5): длина большего объекта не является произведением
## длины меньшего объекта## [1] 4 6 8 7Проблема в том, что эти предупреждения могут в неожиданный момент стать причиной ошибок. Поэтому не стоит полагаться на ресайклинг некратных по длине векторов. См. здесь. А вот ресайклинг кратных по длине векторов — это очень удобная штука, которая используется очень часто.
2.3.4 Индексирование векторов
Итак, мы подошли к одному из самых сложных моментов. И одному из основных. От того, как хорошо вы научись с этим работать, зависит весь ваш дальнейший успех на R-поприще!
Речь пойдет об индексировании векторов. Задача, которую Вам придется решать каждые пять минут работы в R — как выбрать из вектора (или же списка, матрицы и датафрейма) какую-то его часть. Для этого используются квадратные скобочки [] (не круглые — они для функций!).
Самое простое — индексировать по номеру индекса, т.е. порядку значения в векторе.
n <- 1:10
n[1]## [1] 1n[10]## [1] 10Если вы знакомы с другими языками программирования (не MATLAB, там все так же) и уже научились думать, что индексация с 0 — это очень удобно и очень правильно (ну или просто свыклись с этим), то в R Вам придется переучиться обратно. Здесь первый индекс — это 1, а последний равен длине вектора — ее можно узнать с помощью функции
length(). С обоих сторон индексы берутся включительно.
С помощью индексирования можно не только вытаскивать имеющиеся значения в векторе, но и присваивать им новые:
n[3] <- 20
n## [1] 1 2 20 4 5 6 7 8 9 10Конечно, можно использовать целые векторы для индексирования:
n[4:7]## [1] 4 5 6 7n[10:1]## [1] 10 9 8 7 6 5 4 20 2 1Индексирование с минусом выдаст вам все значения вектора кроме выбранных:
n[-1]## [1] 2 20 4 5 6 7 8 9 10n[c(-4, -5)]## [1] 1 2 20 6 7 8 9 10Более того, можно использовать логический вектор для индексирования. В этом случае нужен логический вектор такой же длины:
n[c(T,F,T,F,T,F,T,F,T,F)]## [1] 1 20 5 7 9Ну а если они не равны, то тут будет снова работать правило ресайклинга!
n[c(T,F)] #то же самое - recycling rule!## [1] 1 20 5 7 9Есть еще один способ индексирования векторов, но он несколько более редкий: индексирование по имени. Дело в том, что для значений векторов можно (но не обязательно) присваивать имена:
my_named_vector <- c(first = 1, second = 2, third = 3)
my_named_vector['first']## first
## 1А еще можно “вытаскивать” имена из вектора с помощью функции names() и присваивать таким образом новые.
d <- 1:4
names(d) <- letters[1:4]
d["a"]## a
## 1
letters— это “зашитая” в R константа — вектор букв от a до z. Иногда это очень удобно! Кроме того, есть константаLETTERS— то же самое, но заглавными буквами. А еще есть названия месяцев на английском и числовая константаpi.
Теперь посчитаем среднее вектора n:
mean(n)## [1] 7.2А как вытащить все значения, которые больше среднего?
Сначала получим логический вектор — какие значения больше среднего:
larger <- n>mean(n)
larger## [1] FALSE FALSE TRUE FALSE FALSE FALSE FALSE TRUE TRUE TRUEА теперь используем его для индексирования вектора n:
n[larger]## [1] 20 8 9 10Можно все это сделать в одну строчку:
n[n>mean(n)]## [1] 20 8 9 10Предыдущая строчка отражает то, что мы будем постоянно делать в R: вычленять (subset) из данных отдельные куски на основании разных условий.
2.3.5 NA - пропущенные значения
В реальных данных у нас часто чего-то не хватает. Например, из-за технической ошибки или невнимательности не получилось записать какое-то измерение. Для этого в R есть NA (расшифровывается как Not Available - недоступное значение). NA — это не строка "NA", не 0, не пустая строка "" и не FALSE. NA — это NA. Большинство операций с векторами, содержащими NA будут выдавать NA:
missed <- NA
missed == "NA"## [1] NAmissed == ""## [1] NAmissed == NA## [1] NAЗаметьте: даже сравнение NA c NA выдает NA!
Иногда NA в данных очень бесит:
n[5] <- NA
n## [1] 1 2 20 4 NA 6 7 8 9 10mean(n)## [1] NAЧто же делать?
Наверное, надо сравнить вектор с NA и исключить этих пакостников. Давайте попробуем:
n == NA## [1] NA NA NA NA NA NA NA NA NA NAАх да, мы ведь только что узнали, что даже сравнение NA c NA приводит к NA…
Чтобы выбраться из этой непростой ситуации, используйте функцию is.na():
is.na(n)## [1] FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSEРезультат выполнения is.na(n) выдает FALSE в тех местах, где у нас числа и TRUE там, где у нас NA. Нам нужно сделать наоборот. Здесь нам понадобится оператор ! (мы его уже встречали), который инвертирует логические значения:
n[!is.na(n)]## [1] 1 2 20 4 6 7 8 9 10Ура, мы можем считать среднее!
mean(n[!is.na(n)])## [1] 7.444444Теперь Вы понимаете, зачем нужно отрицание (!)
Вообще, есть еще один из способов посчитать среднее, если есть NA. Для этого надо залезть в хэлп по функции mean():
?mean()В хэлпе мы найдем параметр na.rm =, который по дефолту FALSE. Вы знаете, что нужно делать!
mean(n, na.rm = T)## [1] 7.444444Еееее!
NAможет появляться в векторах других типов тоже. Более того, на самом деле, это все разныеNA: логическийNA,NA_integer_,NA_real_,NA_complex_andNA_character_.
Кроме
NAесть ещеNaN— это разные вещи.NaNрасшифровывается как Not a Number и получается в результате таких операций как0 / 0. Тем не менее, функцияis.na()выдаетTRUEнаNaN, а вот функцияis.nan()выдаетTRUEнаNaNиFALSEнаNA:
is.na(NA)## [1] TRUEis.na(NaN)## [1] TRUEis.nan(NA)## [1] FALSEis.nan(NaN)## [1] TRUE2.3.6 В любой непонятной ситуации — гуглите
Если вдруг вы не знаете, что искать в хэлпе, или хэлпа попросту недостаточно, то… гуглите!

Нет ничего постыдного в том, чтобы гуглить решения проблем. Это абсолютно нормально. Используйте силу интернета во благо и да помогут Вам Stackoverflow4 и бесчисленные R-туториалы!
Computer Programming To Be Officially Renamed “Googling Stack Overflow”
— Stack Exchange ((???)) July 20, 2015
Source: http://t.co/xu7acfXvFF pic.twitter.com/iJ9k7aAVhd
Главное, помните: загуглить работающий ответ всегда недостаточно. Надо понять, как и почему решение работает. Иначе что-то обязательно пойдет не так.
Кроме того, правильно загуглить проблему — не так уж и просто.
Does anyone ever get good at R or do they just get good at googling how to do things in R
— 🔬🖤Lauren M. Seyler, Ph.D.❤️⚒ ((???)) May 6, 2019
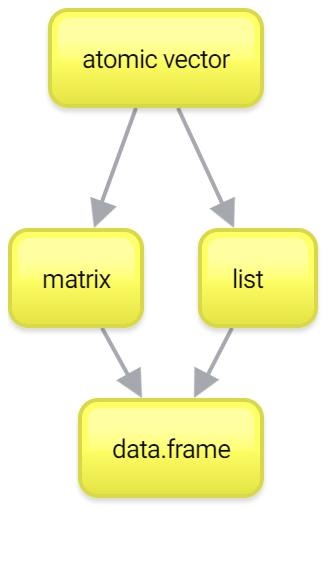
Итак, с векторами мы более-менее разобрались. Помните, что вектора — это один из краеугольных камней вашей работы в R. Если вы хорошо с ними разобрались, то дальше все будет довольно несложно. Тем не менее, вектора — это не все. Есть еще два важных типа данных: списки (list) и матрицы (matrix). Их можно рассматривать как своеобразное “расширение” векторов, каждый в свою сторону. Ну а списки и матрицы нужны чтобы понять основной тип данных в R — data.frame.
2.4 Матрицы (matrix)
Если вдруг вас пугает это слово, то совершенно зря. Матрица — это всего лишь “двумерный” вектор: вектор, у которого есть не только длина, но и ширина. Создать матрицу можно с помощью функции matrix() из вектора, указав при этом количество строк и столбцов.
A <- matrix(1:20, nrow=5,ncol=4)
A## [,1] [,2] [,3] [,4]
## [1,] 1 6 11 16
## [2,] 2 7 12 17
## [3,] 3 8 13 18
## [4,] 4 9 14 19
## [5,] 5 10 15 20Если мы знаем сколько значений в матрице и сколько мы хотим строк, то количество столбцов указывать необязательно:
A <- matrix(1:20, nrow=5)
A## [,1] [,2] [,3] [,4]
## [1,] 1 6 11 16
## [2,] 2 7 12 17
## [3,] 3 8 13 18
## [4,] 4 9 14 19
## [5,] 5 10 15 20Все остальное так же как и с векторами: внутри находится данные только одного типа. Поскольку матрица — это уже двумерный массив, то у него имеется два индекса. Эти два индекса разделяются запятыми.
A[2,3]## [1] 12A[2:4, 1:3]## [,1] [,2] [,3]
## [1,] 2 7 12
## [2,] 3 8 13
## [3,] 4 9 14Первый индекс — выбор строк, второй индекс — выбор колонок. Если же мы оставляем пустое поле вместо числа, то мы выбираем все строки/колонки в зависимости от того, оставили мы поле пустым до или после запятой:
A[, 1:3]## [,1] [,2] [,3]
## [1,] 1 6 11
## [2,] 2 7 12
## [3,] 3 8 13
## [4,] 4 9 14
## [5,] 5 10 15A[2:4, ]## [,1] [,2] [,3] [,4]
## [1,] 2 7 12 17
## [2,] 3 8 13 18
## [3,] 4 9 14 19A[, ]## [,1] [,2] [,3] [,4]
## [1,] 1 6 11 16
## [2,] 2 7 12 17
## [3,] 3 8 13 18
## [4,] 4 9 14 19
## [5,] 5 10 15 20Так же как и в случае с обычными векторами, часть матрицы можно переписать:
A[2:4, 2:4] <- 100
A## [,1] [,2] [,3] [,4]
## [1,] 1 6 11 16
## [2,] 2 100 100 100
## [3,] 3 100 100 100
## [4,] 4 100 100 100
## [5,] 5 10 15 20В принципе, это все, что нам нужно знать о матрицах. Матрицы используются в R довольно редко, особенно по сравнению, например, с MATLAB. Но вот индексировать матрицы хорошо бы уметь: это понадобится в работе с датафреймами.
То, что матрица — это просто двумерный вектор, не является метафорой: в R матрица — это по сути своей вектор с дополнительными атрибутами
dimи (опционально)dimnames. Атрибуты — это свойства объектов, своего рода “метаданные”. Для всех объектов есть обязательные атрибуты типа и длины и могут быть любые необязательные атрибуты. Можно задавать свои атрибуты или удалять уже присвоенные: удаление атрибутаdimу матрицы превратит ее в обычный вектор. Про атрибуты подробнее можно почитать здесь или на стр. 99-101 книги “R in a Nutshell” (???).
2.5 Списки (list)
Теперь представим себе вектор без ограничения на одинаковые данные внутри. И получим список!
l <- list(42, "Пам пам", T)
l## [[1]]
## [1] 42
##
## [[2]]
## [1] "Пам пам"
##
## [[3]]
## [1] TRUEА это значит, что там могут содержаться самые разные данные, в том числе и другие списки и векторы!
lbig <- list(c("Wow", "this", "list", "is", "so", "big"), "16", l)
lbig## [[1]]
## [1] "Wow" "this" "list" "is" "so" "big"
##
## [[2]]
## [1] "16"
##
## [[3]]
## [[3]][[1]]
## [1] 42
##
## [[3]][[2]]
## [1] "Пам пам"
##
## [[3]][[3]]
## [1] TRUEЕсли у нас сложный список, то есть очень классная функция, чтобы посмотреть, как он устроен, под названием str():
str(lbig)## List of 3
## $ : chr [1:6] "Wow" "this" "list" "is" ...
## $ : chr "16"
## $ :List of 3
## ..$ : num 42
## ..$ : chr "Пам пам"
## ..$ : logi TRUEПредставьте, что список - это такое дерево с ветвистой структурой. А на конце этих ветвей - листья-векторы.
Как и в случае с векторами мы можем давать имена элементам списка:
namedl <- list(age = 24, PhDstudent = T, language = "Russian")
namedl## $age
## [1] 24
##
## $PhDstudent
## [1] TRUE
##
## $language
## [1] "Russian"К списку можно обращаться как с помощью индексов, так и по именам. Начнем с последнего:
namedl$age## [1] 24А вот с индексами сложнее, и в этом очень легко запутаться. Давайте попробуем сделать так, как мы делали это раньше:
namedl[1]## $age
## [1] 24Мы, по сути, получили элемент списка — просто как часть списка, т.е. как список длиной один:
class(namedl)## [1] "list"class(namedl[1])## [1] "list"А вот чтобы добраться до самого элемента списка (и сделать с ним что-то хорошее) нам нужна не одна, а две квадратных скобочки:
namedl[[1]]## [1] 24class(namedl[[1]])## [1] "numeric"Indexing lists in #rstats. Inspired by the Residence Inn pic.twitter.com/YQ6axb2w7t
— Hadley Wickham ((???)) September 14, 2015
Как и в случае с вектором, к элементу списка можно обращаться по имени.
namedl[['age']]## [1] 24Хотя последнее — практически то же самое, что и использование знака $.
Списки довольно часто используются в R, но реже, чем в Python. Со многими объектами в R, такими как результаты статистических тестов, удобно работать именно как со списками — к ним все вышеописанное применимо. Кроме того, некоторые данные мы изначально получаем в виде древообразной структуры — хочешь не хочешь, а придется работать с этим как со списком. Но обычно после этого стоит как можно скорее превратить список в датафрейм.
2.6 Data.frame
Итак, мы перешли к самому главному. Самому-самому. Датафреймы (data.frames). Более того, сейчас станет понятно, зачем нам нужно было разбираться со всеми предыдущими темами.
Без векторов мы не смогли бы разобраться с матрицами и списками. А без последних мы не сможем понять, что такое датафрейм.
name <- c("Ivan", "Eugeny", "Lena", "Misha", "Sasha")
age <- c(26, 34, 23, 27, 26)
student <- c(F, F, T, T, T)
df <- data.frame(name, age, student)
df## name age student
## 1 Ivan 26 FALSE
## 2 Eugeny 34 FALSE
## 3 Lena 23 TRUE
## 4 Misha 27 TRUE
## 5 Sasha 26 TRUEstr(df)## 'data.frame': 5 obs. of 3 variables:
## $ name : Factor w/ 5 levels "Eugeny","Ivan",..: 2 1 3 4 5
## $ age : num 26 34 23 27 26
## $ student: logi FALSE FALSE TRUE TRUE TRUEВообще, очень похоже на список, не правда ли? Так и есть, датафрейм — это что-то вроде проименованного списка, каждый элемент которого является atomic вектором фиксированной длины. Скорее всего, список Вы представляли “горизонтально”. Если это так, то теперь “переверните” его у себя в голове на 90 градусов. Так, чтоб названия векторов оказались сверху, а колонки стали столбцами. Поскольку длина всех этих векторов равна (обязательное условие!), то данные представляют собой табличку, похожую на матрицу. Но в отличие от матрицы, разные столбцы могут имет разные типы данных: первая колонка — character, вторая колонка — numeric, третья колонка — logical. Тем не менее, обращаться с датафреймом можно и как с проименованным списком, и как с матрицей:
df$age[2:3]## [1] 34 23Здесь мы сначала вытащили колонку age с помощью оператора $. Результатом этой операции является числовой вектор, из которого мы вытащили кусок, выбрав индексы 2 и 3.
Используя оператор $ и присваивание можно создавать новые колонки датафрейма:
df$lovesR <- T #правило recycling - узнали?
df## name age student lovesR
## 1 Ivan 26 FALSE TRUE
## 2 Eugeny 34 FALSE TRUE
## 3 Lena 23 TRUE TRUE
## 4 Misha 27 TRUE TRUE
## 5 Sasha 26 TRUE TRUEНу а можно просто обращаться с помощью двух индексов через запятую, как мы это делали с матрицей:
df[3:5, 2:3]## age student
## 3 23 TRUE
## 4 27 TRUE
## 5 26 TRUEКак и с матрицами, первый индекс означает строчки, а второй — столбцы.
А еще можно использовать названия колонок внутри квадратных скобок:
df[1:2,"age"]## [1] 26 34И здесь перед нами открываются невообразимые возможности! Узнаем, любят ли R те, кто моложе среднего возраста в группе:
df[df$age < mean(df$age), 4]## [1] TRUE TRUE TRUE TRUEЭту же задачу можно выполнить другими способами:
df$lovesR[df$age < mean(df$age)]## [1] TRUE TRUE TRUE TRUEdf[df$age < mean(df$age), 'lovesR']## [1] TRUE TRUE TRUE TRUEВ большинстве случаев подходят сразу несколько способов — тем не менее, стоит овладеть ими всеми.
Датафреймы удобно просматривать в RStudio. Для это нужно написать команду View(df) или же просто нажать на названии нужной переменной из списка вверху справа (там где Environment). Тогда увидите табличку, очень похожую на Excel и тому подобные программы для работы с таблицами. Там же есть и всякие возможности для фильтрации, сортировки и поиска…5
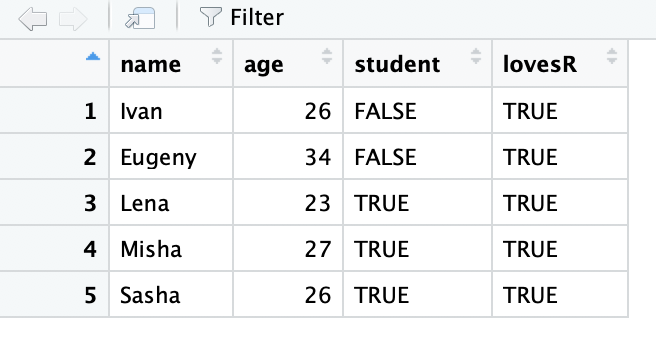
Но, конечно, интереснее все эти вещи делать руками, т.е. с помощью написания кода.
На этом пора заканчивать с введением и приступать к работе с реальными данными.
2.7 Начинаем работу с реальными данными
Итак, пришло время перейти к реальным данным. Мы начнем с использования датасета (так мы будем называть любой набор данных) по Игре Престолов, а точнее, по книгам цикла “Песнь льда и пламени” Дж. Мартина. Да, будут спойлеры, но сериал уже давно закончился и сильно разошелся с книгами…
2.7.1 Рабочая папка и проекты
Для начала скачайте файл по ссылке
Он, скорее всего, появился у Вас в папке “Загрузки”. Если мы будем просто пытаться прочитать этот файл (например, с помощью read.csv() — мы к этой функцией очень скоро перейдем), указав его имя и разрешение, то наткнемся на такую ошибку:
read.csv("character-deaths.csv")## Warning in file(file, "rt"): не могу открыть файл 'character-deaths.csv':
## No such file or directory## Error in file(file, "rt"): не могу открыть соединениеЭто означает, что R не может найти нужный файл. Вообще-то мы даже не сказали, где искать. Нам нужно как-то совместить место, где R ищет загружаемые файлы и сами файлы. Для этого есть несколько способов.
- Магомет идет к горе: перемещение файлов в рабочую папку.
Для этого нужно узнать, какая папка является рабочей с помощью функции getwd() (без аргументов), найти эту папку в проводнике и переместить туда файл. После этого можно использовать просто название файла с разрешением:
got <- read.csv("character-deaths.csv")- Гора идет к Магомету: изменение рабочей папки.
Можно просто сменить рабочую папку с помощью setwd() на ту, где сейчас лежит файл, прописав путь до этой папки. Теперь файл находится в рабочей папке:
got <- read.csv("character-deaths.csv")Этот вариант использовать не рекомендуется. Как минимум, это сразу делает невозможным запустить скрипт на другом компьютере.
- Гора находит Магомета по месту прописки: указание полного пути файла.
got <- read.csv("/Users/Username/Some_Folder/character-deaths.csv")Этот вариант страдает теми же проблемами, что и предыдущий, поэтому тоже не рекомендуется.
Для пользователей Windows есть дополнительная сложность: знак
/является особым знаком для R, поэтому вместо него нужно использовать двойной//.
- Магомет использует кнопочный интерфейс: Import Dataset.
Во вкладке Environment справа в окне RStudio есть кнопка Import Dataset. Возможно, у Вас возникло непреодолимое желание отдохнуть от написания кода и понажимать кнопочки — сопротивляйтесь этому всеми силами, но не вините себя, если не сдержитесь.
- Гора находит Магомета в интернете.
Многие функции в R, предназначенные для чтения файлов, могут прочитать файл не только на Вашем компьютере, но и сразу из интернета. Для этого просто используйте ссылку вместо пути:
got <- read.csv("https://raw.githubusercontent.com/Pozdniakov/stats/master/data/character-deaths.csv")- Каждый Магомет получает по своей горе: использование проектов в RStudio.
File - New Project..., Затем New Directory, New Project, выбираете подходящее Directory Name и нажимаете Create Project.
На первый взгляд это кажется чем-то очень сложным, но это не так. Пользоваться проектами очень просто и ОЧЕНЬ удобно. При создании проекта создается отдельная папочка, где у Вас лежат данные, хранятся скрипты, вспомогательные файлы и отчеты. Если нужно вернуться к другому проекту — просто открываете другой проект, с другими файлами и скриптами. Это еще помогает не пересекаться переменным из разных проектов — а то, знаете, использование двух переменных data в разных скриптах чревато ошибками. Поэтому очень удобным решением будет выделение отдельного проекта под этот курс.
А еще проекты очень удобно работают совместно с системами контроля версий, в частности, с Git. В RStudio есть для этого удобные инструменты. Самый простой способ — при создании проекта
File - New Project...выбратьVersion Control, затем выбрать Git или Subversion и указать ссылку на репозиторий. После этого RStudio его склонирует и все сам настроит. Вот здесь есть подробный туториал по работе с Git и RStudio.
2.7.2 Импорт данных
Как Вы уже поняли, импортирование данных — одна из самых муторных и неприятных вещей в R. Если у Вас получится с этим справиться, то все остальное — ерунда. Мы уже разобрались с первой частью этого процесса — нахождением файла с данными, осталось научиться их читать.
Здесь стоит сделать небольшую ремарку. Довольно часто данные представляют собой табличку. Или же их можно свести к табличке. Такая табличка, как мы уже выяснили, удобно репрезентируется в виде датафрейма. Но как эти данные хранятся на компьютере? Есть два варианта: в бинарном и в текстовом файле.
Текстовый файл означает, что такой файл можно открыть в программе “Блокнот” или ее аналоге и увидеть напечатанный текст: скрипт, роман или упорядоченный набор цифр и букв. Нас сейчас интересует именно последний случай. Таблица может быть представлена как текст: отдельные строчки в файле будут разделять разные строчки таблицы, а какой-нибудь знак-разделитель отделет колонки друг от друга.
Для чтения данных из текстового файла есть довольно удобная функция read.table(). Почитайте хэлп по ней и ужаснитесь: столько разных параметров на входе! Но там же вы увидете функции read.csv(), read.csv2() и некоторые другие — по сути, это тот же read.table(), но с другими дефолтными параметрами, соответствующие формату файла, который мы загружаем. В данном случае используется формат .csv, что означает Comma Separated Values (Значения, Разделенные Запятыми). Это просто текстовый файл, в котором “закодирована” таблица: разные строчки разделяют разные строчки таблицы, а столбцы отделяются запятыми. С этим связана одна проблема: в некоторых странах (в т.ч. и России) принято использовать запятую для разделения дробной части числа, а не точку, как это делается в большинстве стран мира. Поэтому есть “другой” формат .csv, где значения разделены точкой с запятой (;), а дробные значения — запятой (,). В этом и различие функций read.csv() и read.csv2() — первая функция предназначена для “международного” формата, вторая — для (условно) “Российского”.
В первой строчке обычно содержатся названия столбцов — и это чертовски удобно, функции read.csv() и read.csv2() по умолчанию считают первую строчку именно как название для колонок.
Итак, прочитаем наш файл. Для этого используем только параметр file =, который идет первым, и для параметра stringsAsFactors = поставим значение FALSE:
got <- read.csv("data/character-deaths.csv", stringsAsFactors = FALSE)По умолчанию, функции семейства
read.table()читают character переменные как фактор (factor). По сути, факторы — это примерно то же самое, что и character, но закодированные числами. Когда-то это было придумано для экономии используемых времени и памяти: вместо того, чтобы хранить многократно “male” и “female”, можно закодировать их числами 1 и 2, записав отдельно, как расшифровывается 1 и 2. На сегодняшний день факторы обычно становится просто лишней морокой, хотя факторы могут быть удобным инструментом для контроля порядка значений при визуализации данных. Некоторые функции требуют именно character, некоторые factor, в большинстве случаев это без разницы. Но иногда непонимание может привести к дурацким ошибкам. В данном случае мы просто пока обойдемся без факторов.
Можете проверить с помощью View(got): все работает! Если же вылезает какая-то странная ерунда или же просто ошибка — попробуйте другие функции и покопаться с параметрами. Для этого читайте Help.
Кроме .csv формата есть и другие варианты хранения таблиц в виде текста. Например, .tsv — тоже самое, что и .csv, но разделитель — знак табуляции. Для чтения таких файлов есть функция read.delim() и read.delim2(). Впрочем, даже если бы ее и не было, можно было бы просто подобрать нужные параметры для функции read.table(). Есть даже функции (например, fread() из пакета data.table — мы ее будем использовать завтра!), которые пытаются сами “угадать” нужные параметры для чтения — часто они справляются с этим довольно удачно. Но не всегда. Поэтому стоит научиться справляться с любого рода данными на входе.
Тем не менее, далеко не всегда таблицы представлены в виде текстового файла. Самый распространенный пример таблицы в бинарном виде — родные форматы Microsoft Excel. Если Вы попробуете открыть .xlsx файл в Блокноте, то увидите кракозябры. Это делает работу с этим файлами гораздо менее удобной, поэтому стоит избегать экселевских форматов и стараться все сохранять в .csv.
Для работы с экселевскими файлами есть много пакетов: readxl, xlsx, openxlsx. Для чтения файлов SPSS, Stata, SAS есть пакет foreign. Что такое пакеты и как их устанавливать мы изучим позже.
При первом запуске RStudio вы не увидите это окно. Для того, чтобы оно появилось, нужно нажать
File - New File - R Script.↩В RStudio есть много удобных сочетаний горячих клавиш. Чтобы посмотреть их все, нажмите
Help - Keyboard Shortcuts Help.↩Во время написания кода вам может казаться понятным то, что вы написали, но при возвращении к коду через некоторое время вы уже не будете этого помнить. Старайтесь писать комментарии как можно чаще!↩
Stackoverflow — это сайт с вопросами и ответами. Эдакий аналог Quora, The Question, ну или Ответы Mail.ru в мире программирования.↩
Все, что вы нажмете в этом окошке, никак не повлияет на исходную переменную. Так что можете смело использовать эти функции для исследования содержимого датафрейма.↩