4 День 3. Описательная статистика и визуализация

4.1 Описательная статистика

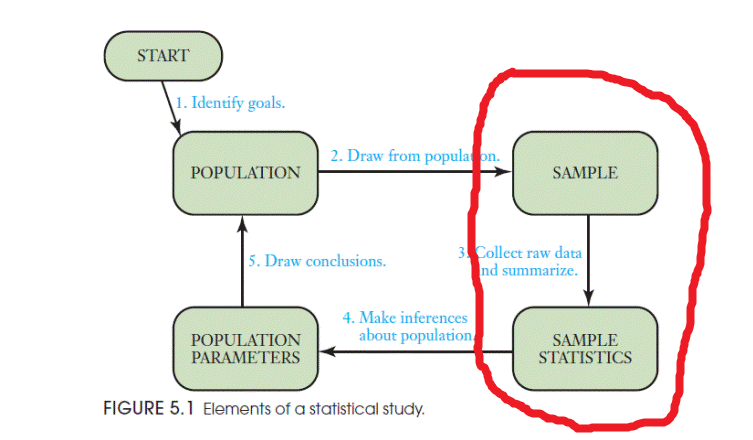
Статистика делится на описательную статистику (descriptive statistics) и статистику вывода (inferential statistics). Описательная статистика пытается описать нашу выборку (sample, т.е. те данные, что у нас на руках) различными способами. Проблема в том, что описательная статистика может описать только то, что у нас есть, но не позволяет сделать выводы о генеральной совокупности (population) - это уже цель статистики вывода. Цель описательной статистики - “ужать” данные для их обобщенного понимания с помощью статистик.

Заметьте, у выборки (sample) мы считаем статистики (statistics), а у генеральной совокупности (Population) есть параметры (Parameters). Вот такая вот мнемотехника.

Статистики часто выступают в роли точечной оценки (point estimators) параметров, так что в этом легко запутаться. Например, среднее (в выборке) - это оценка среднего (в генеральной совокупности). Да, можно свихнуться. Мы это будем разбирать подробнее в следующие занятия (это действительно важно, поверьте), пока что остановимся только на описании выборки.

Сегодня мы будем работать с пакетом survival, в котором есть датасет pbc. Мы его сразу превратим в data.table

library(survival)
library(data.table)

data(pbc)
pbcdt <- as.data.table(pbc)

Это данные 424 пациентов с первичным билиарным циррозом - редким аутоимунным заболеванием печени. При поступлении в клинику у них измерили разные медицинские показатели, определели в экспериментальную и контрольную группу. В наборе данных есть информация о том, что стало с этими испытуемыми.

“This data is from the Mayo Clinic trial in primary biliary cirrhosis (PBC) of the liver conducted between 1974 and 1984. A total of 424 PBC patients, referred to Mayo Clinic during that ten-year interval, met eligibility criteria for the randomized placebo controlled trial of the drug D-penicillamine. The first 312 cases in the data set participated in the randomized trial and contain largely complete data.”

Подробнее про датасет можно почитать здесь или в Help.

Эти данные часто используются в качестве примера для анализа выживаемости. Они уже в достаточно упорядоченном виде и не нуждаются в предобработке (что, к сожалению, случай малореалистичный).

Для простоты мы удалим все пропущенные значения. Мы уже знакомы с функцией is.na(), теперь познакомимся с еще одной функцией: complete.cases() возвращает вектор, равный длине датафрейма, с FALSE для строчек, где есть хотя бы один NA, и TRUE если пропущенных значений нет.

pbcdt <- pbcdt[complete.cases(pbc),]

Пока что мы будем использовать только данные о возрасте испытуемых. Для краткости обозначим это вектором a

a <- pbcdt$age

4.1.1 Меры центральной тенденции

Мера центральной тенденции - это число для описания центра распределения.

4.1.1.1 Арифметическое среднее

Самая распространенная мера центральных тенденций - арифметическое среднее, то самое, которые мы считаем с помощью функции mean().

\[\overline{x}= \frac{\sum\limits_{i=1}^{n} x_{i}} {n}\]

Не пугайтесь значка \[\sum\limits_{i=1}^{n}\] - это означает сумму от i = 1 до n. Что-то вроде цикла for!

В качестве упражнения попробуйте самостоятельно превратить эту формулу в функцию mymean() c помощью sum() и length(). Можете убирать NA по дефолту! Сравните с результатом функции mean().

mean(a)

## [1] 49.79966

4.1.1.2 Медиана

Медиана - это середина распределения. Представим, что мы расставили значения по порядку (от меньшего к большему) и взяли значение по середине. Если у нас четное количество значений, то берется среднее значение между теми двумя, что по середине. Для расчета медианы есть функция median():

median(a)

## [1] 49.70979

Разница медианы со средним не очень существенная. Это значит, что распределение довольно “симметричное”. Но бывает и по-другому.

Представьте себе, что кто-то говорит про среднюю зарплату в Москве. Но ведь эта средняя зарплата становится гораздо больше, если учитывать относительно небольшое количество мультимиллионеров и миллиардеров! А вот медианная зарплата будет гораздо меньше.

Представьте себе, что в эту клинику с циррозом печени пришел 8000-летний Король Ночи из Игры Престолов. Тогда арифметическое среднее станет гораздо больше:

mean(c(a, 8000))

## [1] 78.50075

А вот медиана останется почти той же.

median(c(a, 8000))

## [1] 49.76318

Таким образом, экстремально большие или маленькие значения оказывают сильное влияние на арифметическое среднее, но не на медиану. Поэтому медиана считается более “робастной” оценкой, т.е. более устойчивой к выбросам и крайним значениям.

4.1.1.3 Усеченное среднее (trimmed mean)

Если про среднее и медиану слышали все, то про усеченное (тримленное) среднее известно гораздо меньше. Тем не менее, на практике это довольно удобная штука, потому что представляет собой некий компромисс между арифметическим средним и медианой.

В усеченном среднем значения ранжируются так же, как и для медианы, но отбрасывается только какой-то процент крайних значений. Усеченное среднее можно посчитать с помощью обычной функции mean(), поставив нужное значение параметра trim =:

mean(a, trim = 0.1)

## [1] 49.57392

trim = 0.1 означает, что мы отбросили 10% слева и 10% справа. trim может принимать значения от 0 до 0.5. Что будет, если trim = 0?

mean(a, trim = 0)

## [1] 49.79966

Обычное арифметическое среднее! А если trim = 0.5?

mean(a, trim = 0.5)

## [1] 49.70979

Медиана!

4.1.1.4 Мода

Мода (mode) - это самое частое значение. Обычно используется для номинальных переменных. Например, можно посчитать моду для регионов, в которых происходили битвы. Что интересно, в R нет встроенной функции для подсчета моды. Обычно она и не нужна: мы можем посчитать таблицу частот и даже проранжировать ее (и мы уже умеем это делать разными способами). На случай если Вы все-таки хотите создать свою функцию для моды, можно попробовать что-то такое:

mymode <- function(x){names(which.max(table(x)))}
mymode(pbcdt$sex)

## [1] "f"

4.1.2 Меры рассеяния

Начинающий статистик пытался перейти в брод реку, средняя глубина которой 1 метр. И утонул.
В чем была его ошибка? Он не учитывал разброс значений глубины!

Мер центральной тенденции недостаточно, чтобы описать выборку. Необходимо знать ее вариабельность.

4.1.2.1 Размах {range}

Самое очевидное - посчитать размах (range), то есть разницу между минимальным и максимальным значением. В R есть функция для вывода максимального и минимального значений:

range(a)

## [1] 26.27789 78.43943

Осталось посчитать разницу между ними:

diff(range(a))

## [1] 52.16153

Естественно, крайние значения очень сильно влияют на этот размах, поэтому на практике он не очень-то используется.

4.1.2.2 Дисперсия

Дисперсия (variance) вычисляется по следующей формуле:

\[s^2= \frac{\sum\limits_{i=1}^{n} (x_{i} - \overline{x})^2} {n}\]

Попробуйте превратить это в функцию myvar()!

myvar <- function(x) mean((x - mean(x))^2)

Естественно, в R уже есть готовая функция var(). Но, заметьте, ее результат немного отличается от нашего:

myvar(a)

## [1] 110.334

var(a)

## [1] 110.7353

Дело в том, что встроенная функция var() делит не на \(n\), а на \(n-1\). Это связано с тем, что эта функция пытается оценить дисперсию в генеральной совокупности, т.е. относится уже к статистике вывода. Про это мы будем говорить в дальнейших занятиях, сейчас нам нужно только отметить то, что здесь есть небольшое различие.

4.1.2.3 Стандартное отклонение

Если вы заметили, значение дисперсии очень большое. Чтобы вернуться к единицам измерения, соответствующих нашим данным используется корень из дисперсии, то есть стандартное отклонение (standard deviation):

\[s= \sqrt\frac{\sum\limits_{i=1}^{n} (x_{i} - \overline{x})^2} {n}\]

Для этого есть функция sd():

sd(a)

## [1] 10.52308

Что то же самое, что и:

sqrt(var(a))

## [1] 10.52308

4.1.2.4 Медианное абсолютное отклонение

Поскольку стандартное отклонение не устойчово ко всяким выбросам, то иногда используют его альтернативу, которая устойчива к выбросам (особенно если эти выбросы нам как раз и нужно удалить) - медианное абсолютное отклонение (median absolute deviation):

\[mad= median(|x_{i} - median(x)|)\]

Для этого есть функция mad():

mad(a)

## [1] 10.63291

4.1.2.5 Межквартильный размах

Другой вариант рабостной оценки вариабельности данных является межквартильный размах (interquartile range, IQR). Это разница между третьим и первым квартилем⁷ - значением, которое больше 75% значений в выборке, и значением, которое больше 25% значений в выборке.

IQR(a)

## [1] 15.07187

Ну а второй квартиль - это медиана!

4.1.3 Ассиметрия и эксцесс

4.1.3.1 Ассиметрия

Ассиметрия (skewness) измеряет симметричность распределения. Положительный показатель ассиметрии (“Right-skewed” или positive skewness) означает, что хвосты с правой части распределения длиннее. Негативный показатель ассиметрии (“Left-skewed” или negative skewness) означает, что левый хвост длиннее.

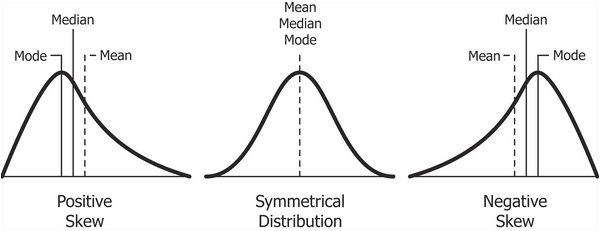
Например, в психологии положительная ассиметрия встречается очень часто. Например, время реакции: оно ограничено снизу 0 мс (а по факту не меньше 100 мс - быстрее сигнал не успеет по нервной системе пройти до пальцев), а вот с другой стороны оно никак не ограничено. Испытуемый может на полчаса перед монитором затупить, ага.

4.1.3.2 Эксцесс

Эксцесс (kurtosis) - это мера “вытянутости” распределения:

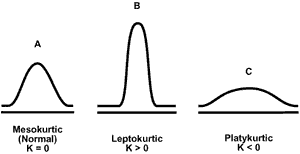
Положительные показатели эксцесса означают “вытянутое” распределение, а отрицательные - “плоское”.

4.1.3.3 Ассиметрия и эксцесс в R

К сожалению, в базовом R нет функций для ассиметрии и эксцесса. Зато есть замечательный пакет psych (да-да, специально для психологов).

install.packages("psych")

library("psych")

В нем есть функции skew() и kurtosi():

skew(a)

## [1] 0.1786867

kurtosi(a)

## [1] -0.5174814

Ассиметрия близка к нулю - значит распределение выборки достаточно симметричное, а эксцесс немного ниже нуля - значит распределение довольно “плоское”.

4.1.4 А теперь все вместе!

В базовом R есть функция summary(), которая позволяет получить сразу неплохой набор описательных статистик.

summary(a)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   26.28   41.51   49.71   49.80   56.58   78.44

Функция summary() - это универсальная (generic) функция. Это означает, что Вы можете ее применять для разных объектов и получать разные результаты. Попробуйте применить ее к векторам с разными типами данных и даже к дата.фреймам и дата.тейблам. Посмотрите, что получится.

В пакете psych есть еще и замечательная функция describe(), которая даст Вам еще больше статистик, включая ассиметрию и куртозис:

describe(a)

##    vars   n mean    sd median trimmed   mad   min   max range skew
## X1    1 276 49.8 10.52  49.71   49.57 10.63 26.28 78.44 52.16 0.18
##    kurtosis   se
## X1    -0.52 0.63

Даже усеченное (trimmed) среднее есть (с trim = 0.1)! Все кроме se мы уже знаем. А про этот se узнаем через позже.

Эта функция прекрасно работает в data.table в сочетании с by =:

pbcdt[, describe(age), by = stage]

##    stage vars   n     mean       sd   median  trimmed       mad      min
## 1:     4    1  94 53.09709 10.71781 53.92334 53.20437 10.890666 29.55510
## 2:     3    1 111 47.94154 10.00419 47.42779 47.41838  9.948946 26.27789
## 3:     2    1  59 48.52757 10.22616 48.75838 48.34855 10.975908 30.27515
## 4:     1    1  12 47.41182 10.11477 47.97673 47.75359 12.132762 28.88433
##         max    range        skew   kurtosis       se
## 1: 78.43943 48.88433 -0.07684694 -0.4361883 1.105458
## 2: 71.89322 45.61533  0.35465904 -0.3655477 0.949556
## 3: 75.01164 44.73648  0.19440406 -0.7000602 1.331333
## 4: 62.52156 33.63723 -0.06406915 -1.1025021 2.919883

4.1.5 Описательных статистик недостаточно

Я в тайне от Вас загрузил данные в переменную xxx (можете найти этот набор данных здесь, если интересно). Выглядят они примерно так:

head(xxx)

##          x       y
## 1: 55.3846 97.1795
## 2: 51.5385 96.0256
## 3: 46.1538 94.4872
## 4: 42.8205 91.4103
## 5: 40.7692 88.3333
## 6: 38.7179 84.8718

str(xxx)

## Classes 'data.table' and 'data.frame':   142 obs. of  2 variables:
##  $ x: num  55.4 51.5 46.2 42.8 40.8 ...
##  $ y: num  97.2 96 94.5 91.4 88.3 ...
##  - attr(*, ".internal.selfref")=<externalptr>

Надеюсь, Вы уже понимаете, как это интерпретировать - два столбца с 142 числами каждый. Представьте себе, как выглядят эти точки на плоскости, если каждая строчка означают координаты одной точки по осям x и y (это называется диаграмма рассеяния, точечная диаграмма или scatterplot).

Применим разные функции, которые мы выучили:

mean(xxx$x)

## [1] 54.26327

mean(xxx$y)

## [1] 47.83225

median(xxx$x)

## [1] 53.3333

median(xxx$y)

## [1] 46.0256

Средние и медианы примерно одинаковые, при этом по х они около 53-54, а по у - примерно 46-47. Попытайтесь представить это. Идем дальше:

sd(xxx$x)

## [1] 16.76514

sd(xxx$y)

## [1] 26.9354

Похоже, расброс по у несколько больше, верно?

skew(xxx$x)

## [1] 0.2807568

skew(xxx$y)

## [1] 0.2472603

kurtosi(xxx$x)

## [1] -0.2854912

kurtosi(xxx$y)

## [1] -1.063552

Похоже, оба распределения немного право-ассиметричны и довольно “плоские”.

Давайте еще посчитаем корреляцию. Мы про нее будем говорить позже гораздо подробнее. Пока что нам нужно знать, что она говорит о линейной связи двух переменных. Если корреляция положительная (максимум равен 1), то чем больше х, тем больше у. Если отрицательная (минимум равен -1), то чем больше х, тем меньше у. Если же корреляция равна нулю, то такая линейная зависимость отсутствует.

cor(xxx$x, xxx$y)

## [1] -0.06447185

Корреляция очень близка к нулю (делайте выводы и представляйте).

Давайте напоследок воспользуемся функцией describe() из psych:

describe(xxx)

##   vars   n  mean    sd median trimmed   mad   min   max range skew
## x    1 142 54.26 16.77  53.33   53.69 15.97 22.31 98.21 75.90 0.28
## y    2 142 47.83 26.94  46.03   46.90 30.79  2.95 99.49 96.54 0.25
##   kurtosis   se
## x    -0.29 1.41
## y    -1.06 2.26

Готовы узнать, как выглядят эти данные на самом деле?!

Жмите сюда если готовы!

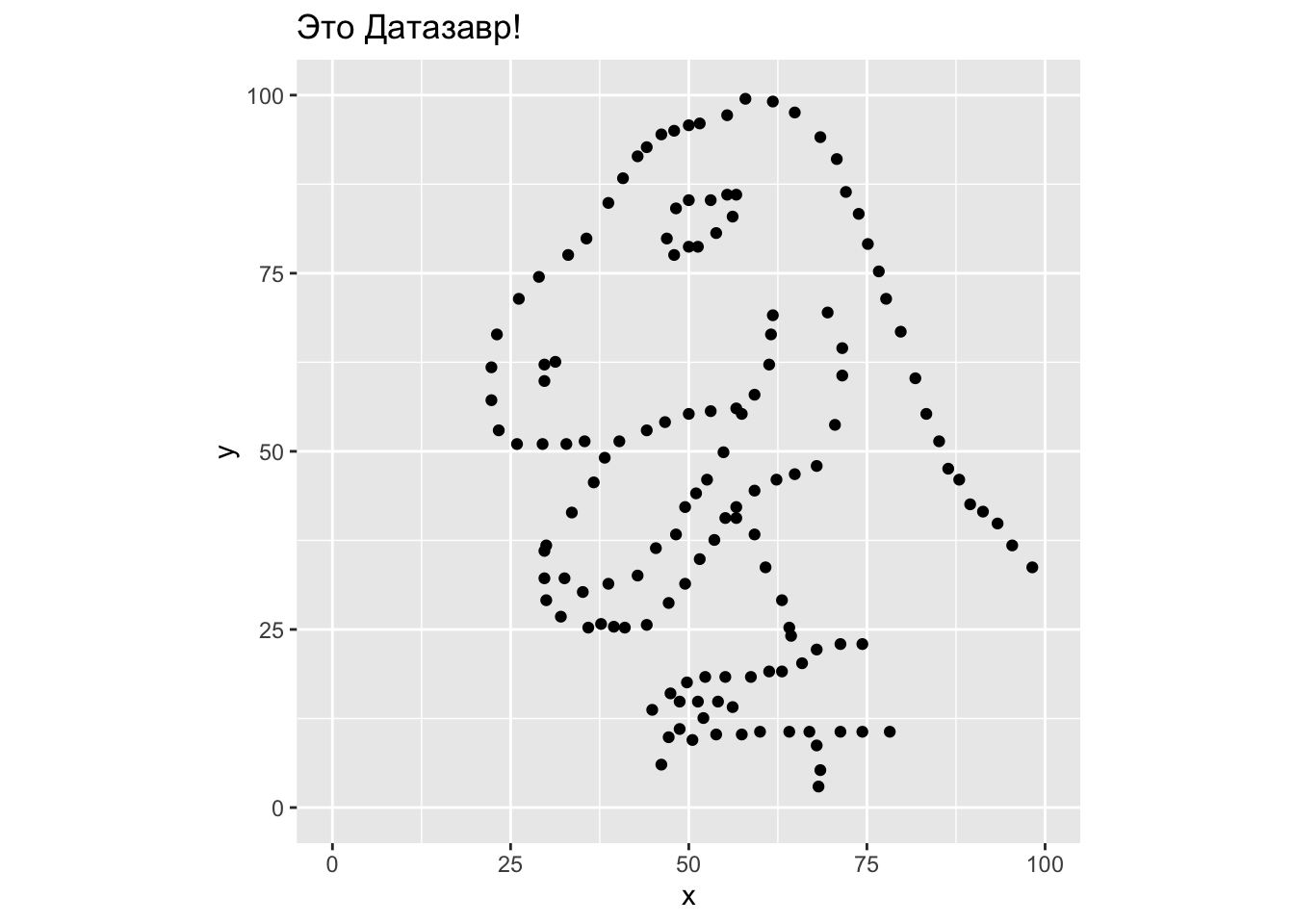
Из этого можно сделать важный вывод: не стоит слепо доверять описательным статистикам. Нужно визуализировать данные, иначе можно попасть в такую ситуацию в реальности. Все следующее занятие будет посвящено визуализации данных.

4.2 Визуализация данных в R

4.2.1 Базовые функции для графики

В R есть достаточно мощный встроенный инструмент для визуализации. Я приведу три простых примера. Во-первых, это та самая диаграмма рассеяния. Здесь все просто: функция plot(), вектора x и у, дополнительные параметры для цвета, размера, формы точек.

Для примера возьмем из дататейбла pbcdt уровень холистерина и возраст:

plot(pbcdt$age, pbcdt$chol)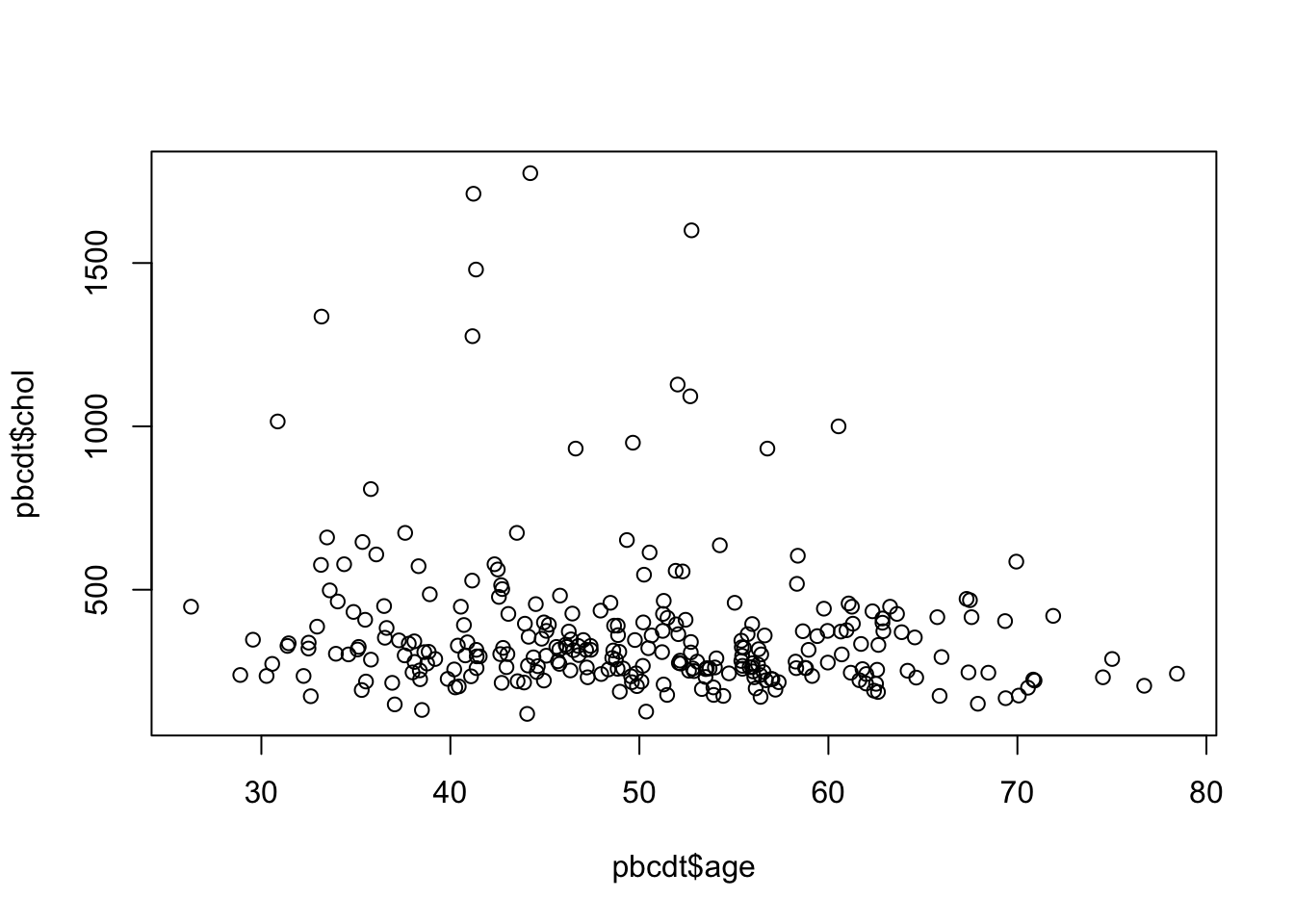

Между прочим, функция plot() - это тоже универсальная (generic) функция, как и summary(). В качестве аргумента можете ей скормить просто один вектор, матрицу, датафрейм. Более того, многие пакеты добавляют новые методы plot() для новых объектов из этих пакетов.

Другая распространенная функция - hist() - гистограмма:

hist(pbcdt$age)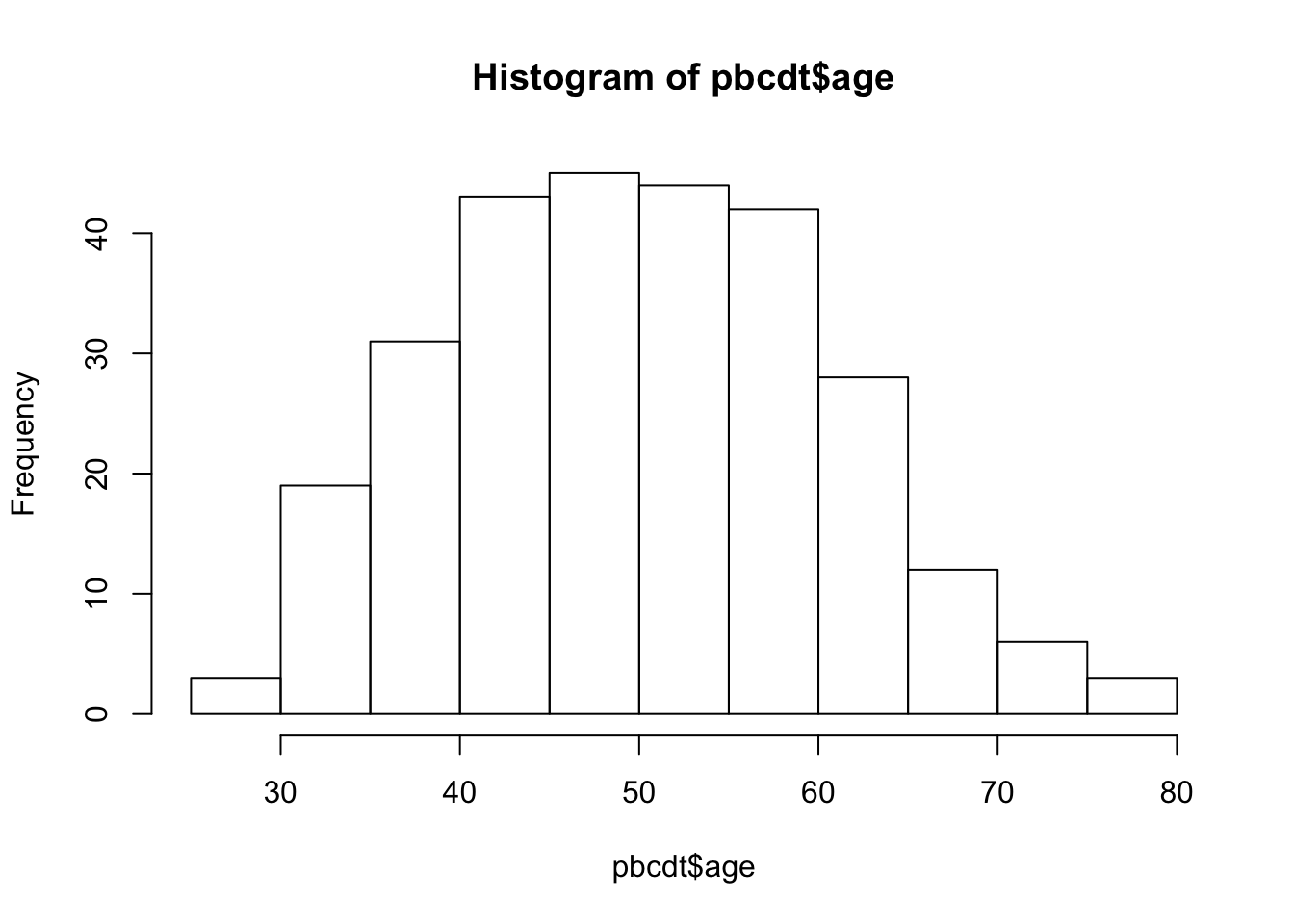

Ну и закончим на суперзвезде прошлого века под названием “ящик с усами”(boxplot with whiskers):

boxplot(chol ~ stage, pbcdt)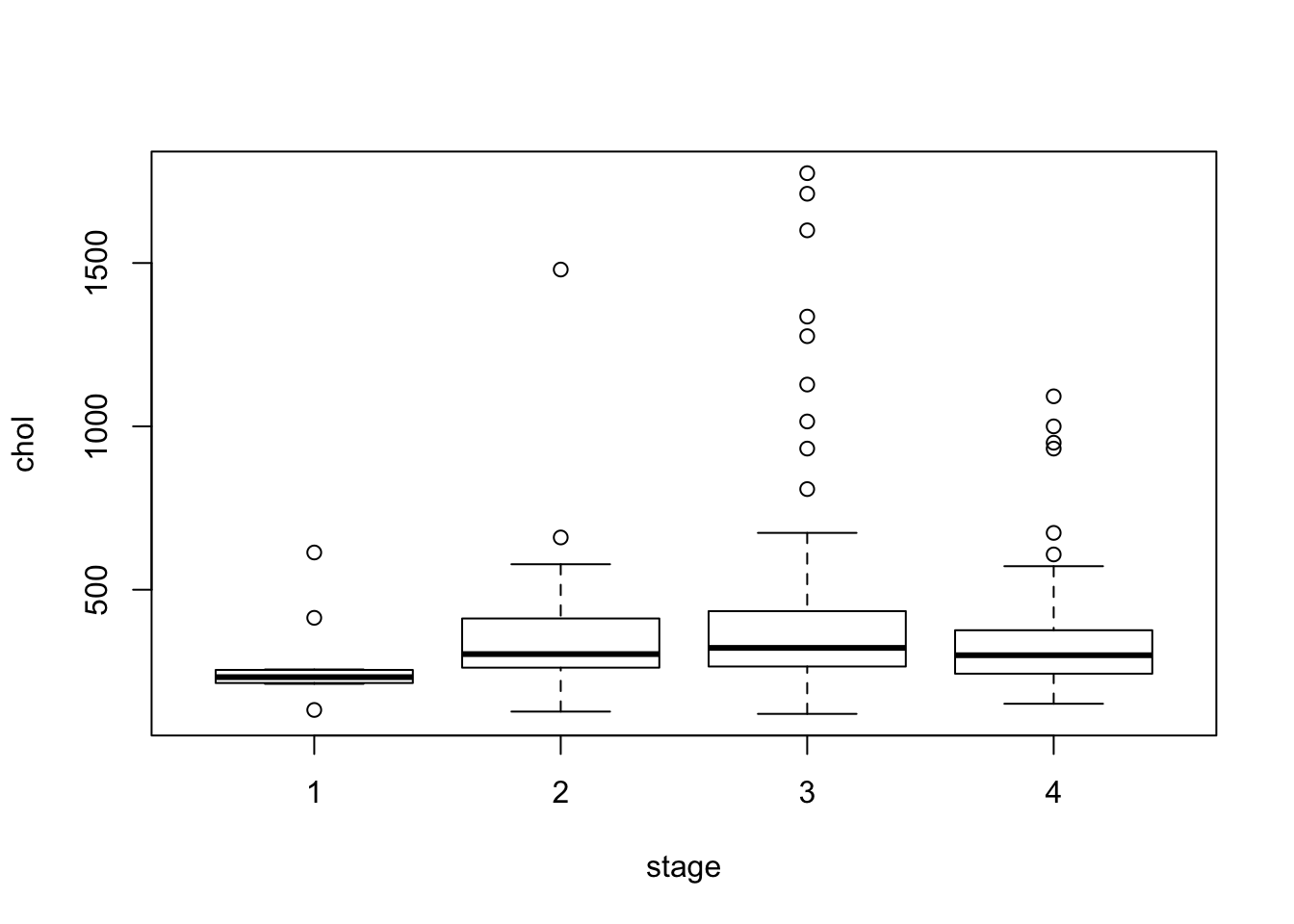

Здесь мы использовали уже знакомый нам класс формул. Они еще будут нам встречаться дальше, обычно они используются следующим образом: слева от ~ находится зависимая переменная, а справа - “предикторы”. Эта интуиция работает и здесь: мы хотим посмотреть, как различается холестирин в зависимости от стадии.

4.2.2 ggplot2

gg в ggplot2 означает Grammar of Graphics - это книга Леланда Уилкинсона, в которой он попытался создать язык описания и создания всевозможных визуализаций. Хэдли Викхэм (уже знакомый нам по dplyr) дополнил эту систему (Layered Grammar of Graphics) и реализовал в качестве пакета в R под названием ggplot2.

install.packages("ggplot2")

library(ggplot2)

4.2.2.1 Layered Grammar of Graphics

Основные элементы Layered Grammar of Graphics

• Layer (geom +)
• Scale
• Coordinate system (coord)
• Faceting (facet)
• Theme
• Defaults
  • Data
  • Mapping

-Layer: - Data - Mapping (aes) - Statistical transformation (stat) - Geometric object (geom) - Position adjustment (position)

4.2.2.2 Пример 0: Круговая диаграмма

Чтобы продемонстрировать суть “графической грамматики” Уилкинсон в своей книге приводит в качестве примера круговую диаграмму. Да-да, тот самый злополучный пирог, которым все так плюются! Тем не менее, этот пример перевернет Ваше понимание графиков с ног на голову.

Итак, создадим объект ggplot с данными и каким-нибудь мэппингом по умолчанию (пока не обращайте внимания на него). Если мы попробуем это отрисовать, то получим пустой экран.

pie <- ggplot(data = pbcdt, aes(x = "", fill = sex))
pie

Теперь мы добавим на картинку геом, который будет наследовать мэппинг и набор данных, указанные в ggplot(). Этим геомом будет geom_bar(), для столбиковой диаграммы. Мы получаем немного странный график:

pie <- pie +
  geom_bar(position = "fill")
pie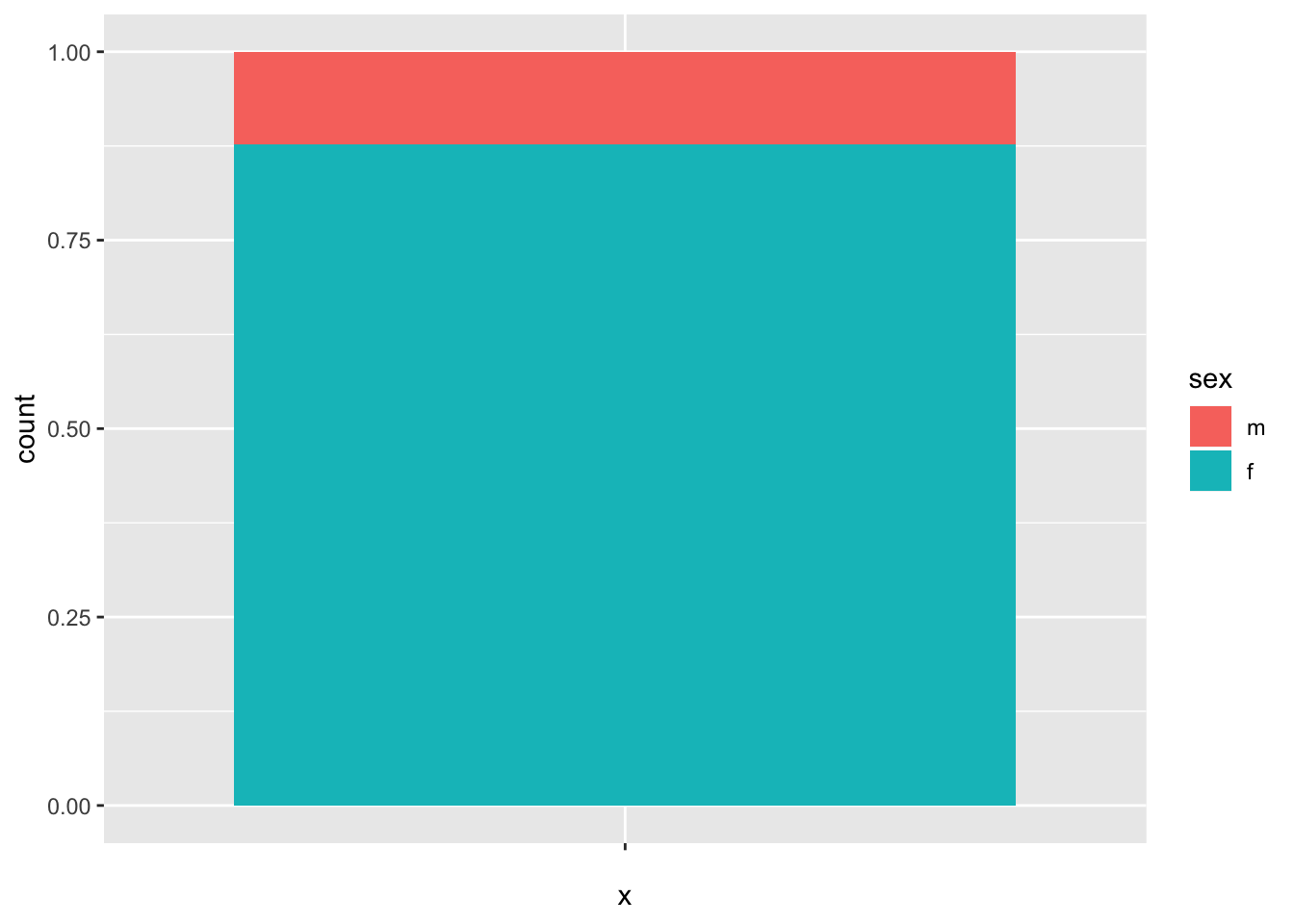

Как нам из этого получить круговую диаграмму? Надо поменять декартову систему координат на полярную (круговую)!

pie + coord_polar(theta = "y")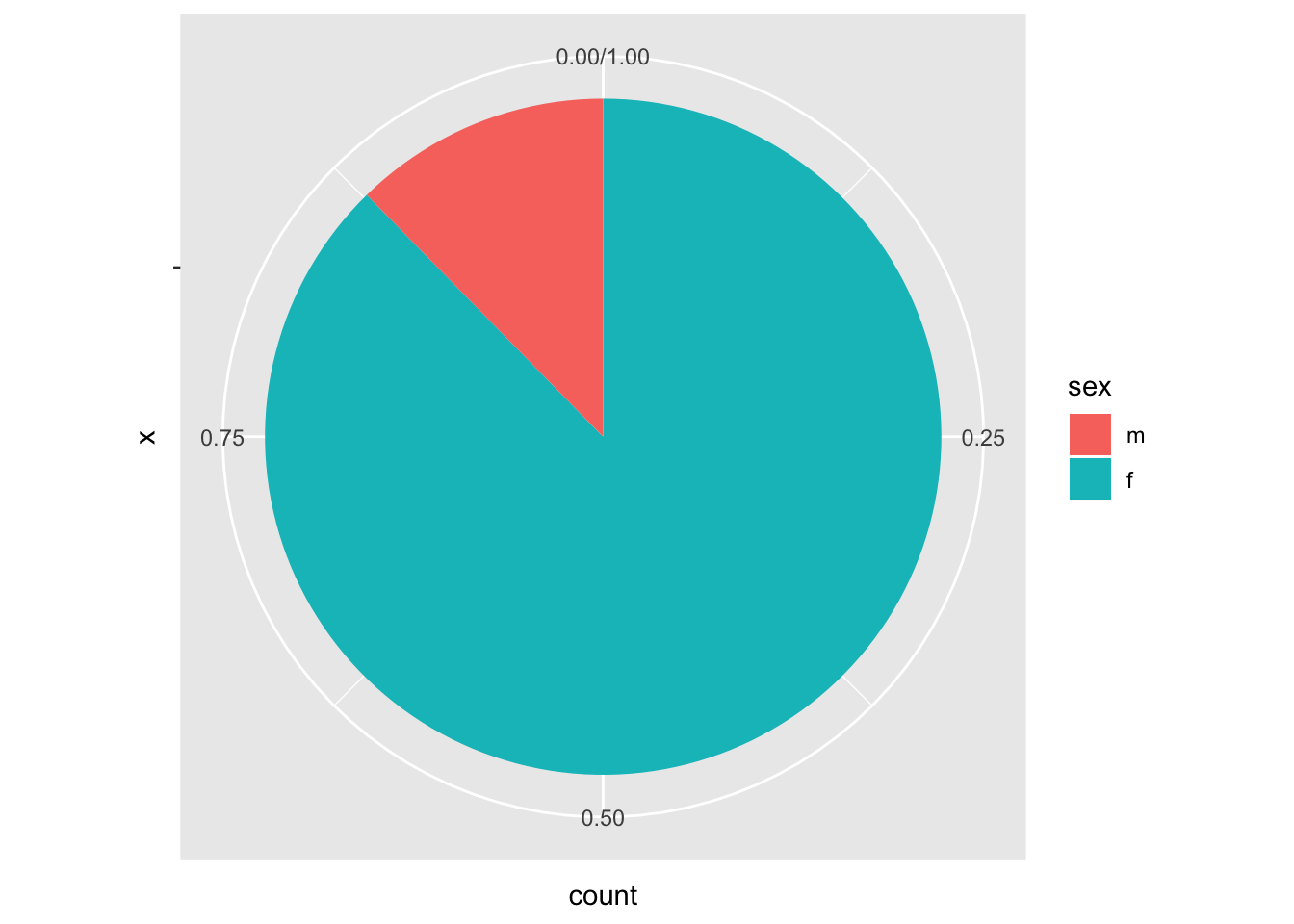

В качестве финального штриха мы можем максимально упростить тему:

pie + coord_polar(theta = "y")+theme_void()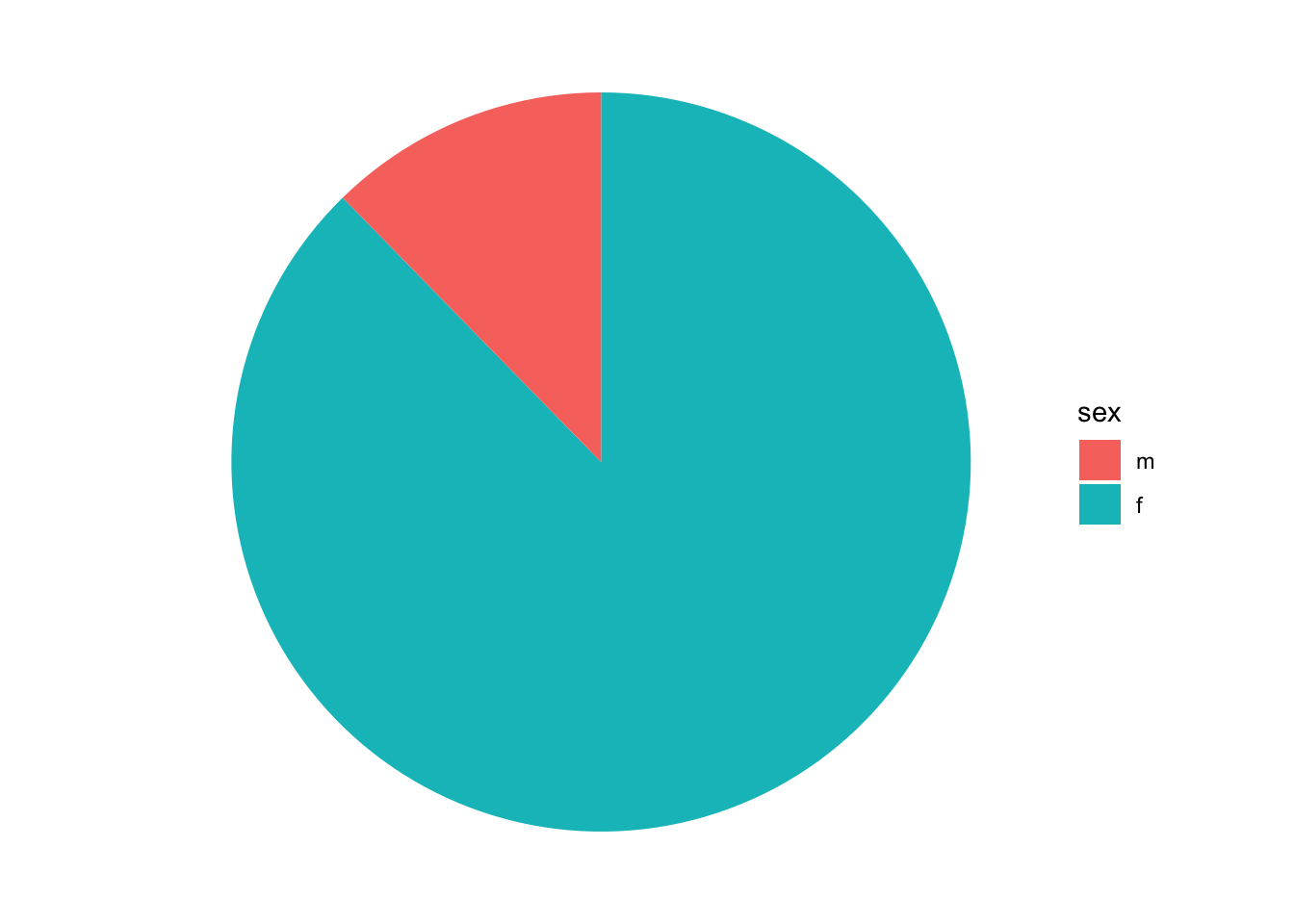

То есть пай-чарт можно рассматривать не как отдельный вид графика, а как столбчатую диаграмму в полярной системе координат. То же верно и для многих других графиков, которые можно представить с помощью ограниченного количества геомов и других элементов грамматики графики. Подумайте над этим!

4.2.2.3 Пример 1: Диаграмма рассеяния

Итак, давайте разбираться детально с синтаксисом ggplot2.

Для начала создадим объект ggplot с помощью ggplot() команды. Для нее можно указать данные и мэппинг по умолчанию с помощью аргументов data = и mapping = aes()

В качестве примера мы сделаем диаграмму рассеяния с возрастом по х и уровнем холестирина по у:

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))

На самом деле, название параметров data = и mapping = можно опустить.

Наш график пуст. Нам нужно сделать слой с нужной геометрией. В данном случае - geom_point(). Синтаксис ggplot() несколько необычный - мы добавляем новые слои и дополнительные параметры с помощью +:

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point()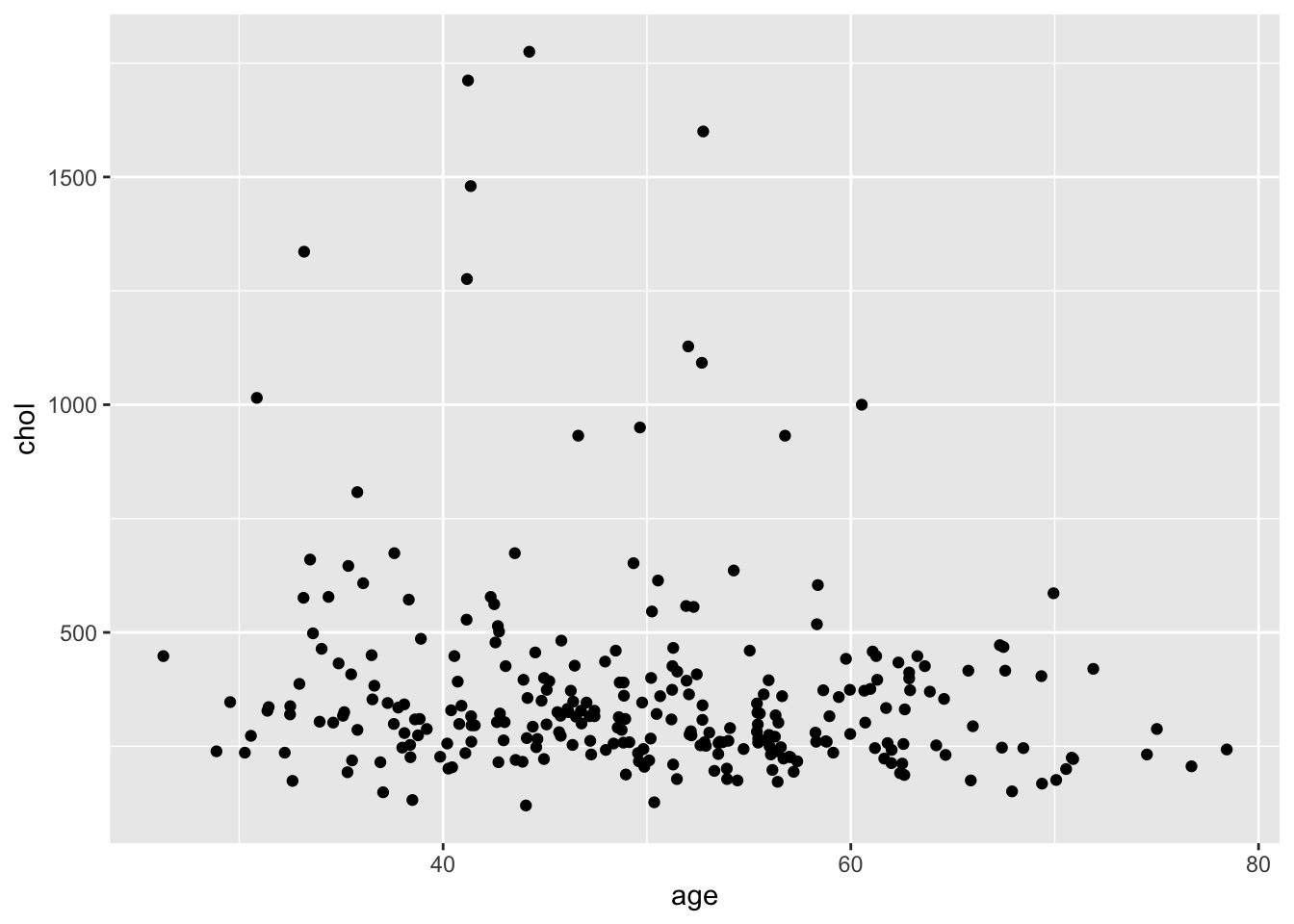

4.2.2.3.1 Фиксированные параметры vs mapping aesthetics

Теперь нам хотелось бы как-то разнообразить график. Изменить цвет, форму, размер точек:

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 3, colour = "purple", shape = 15)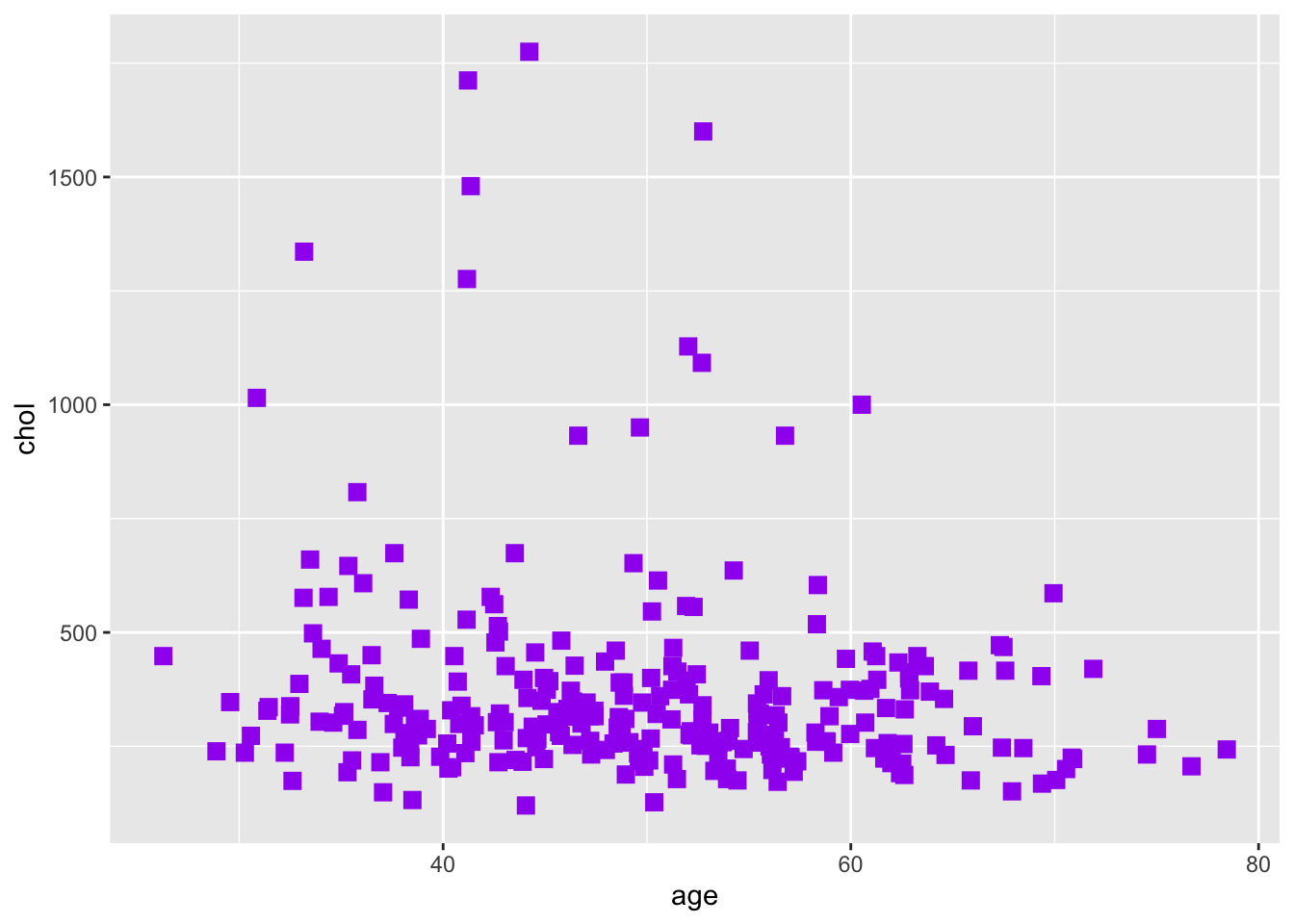

А что если мы хотим сделать параметры геома поставить в зависимость от данных? Тогда нам нужно менять мэппинг с помощью эстетики - aes():

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 3,aes(colour = sex, shape = as.factor(hepato)))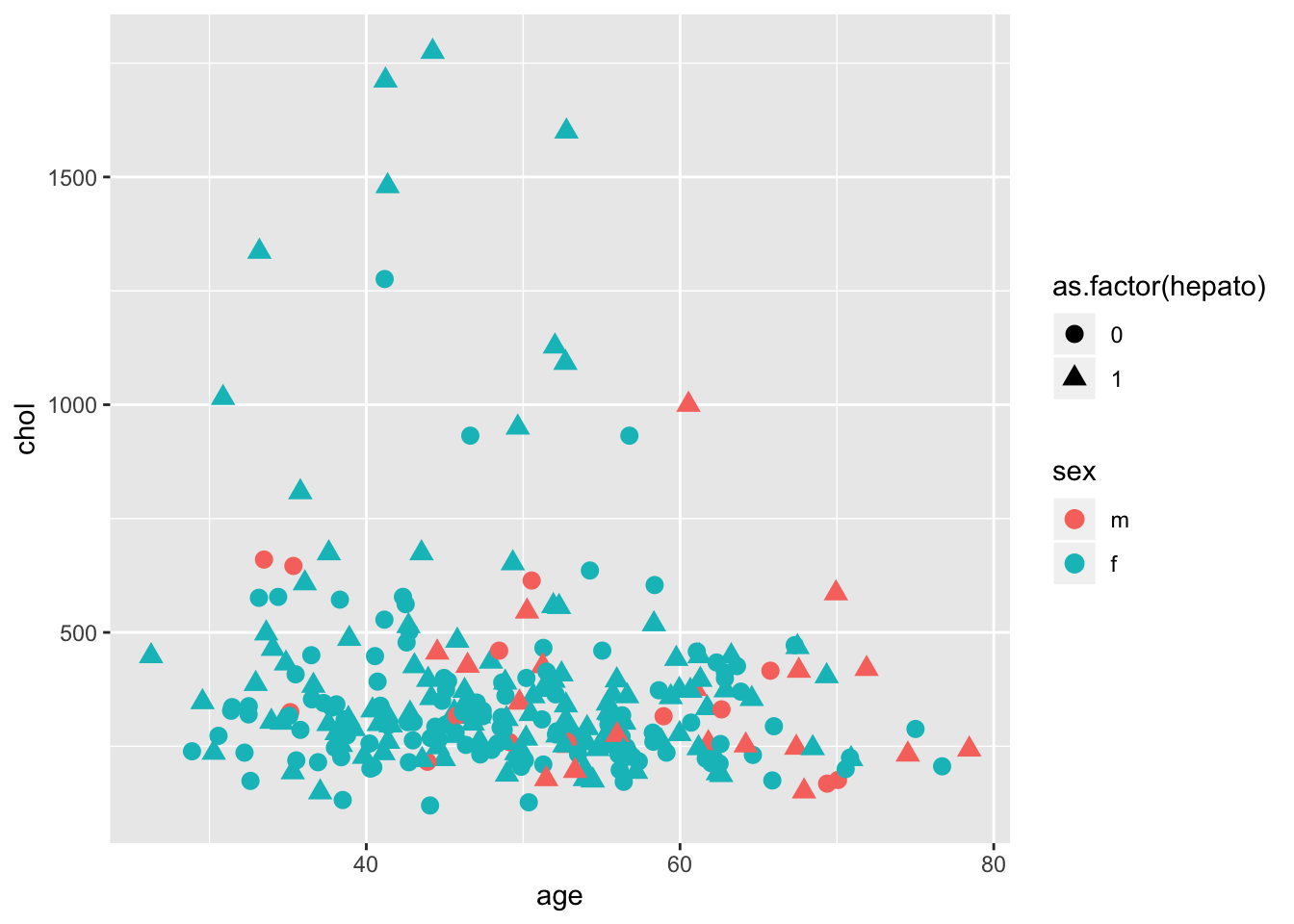

Если какой-то параметр зависит от данных, то он прописывается внутри aes(), если же это фиксированное значение - то он находится “извне” функции aes() (параметра mapping =).

Здесь мы hepato (является печень увеличенной или нет) превратили в фактор. Иначе ggplot2 воспринимает эту колонку как континуальную переменную, потому что она numeric.

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 2,aes(shape = as.factor(hepato)))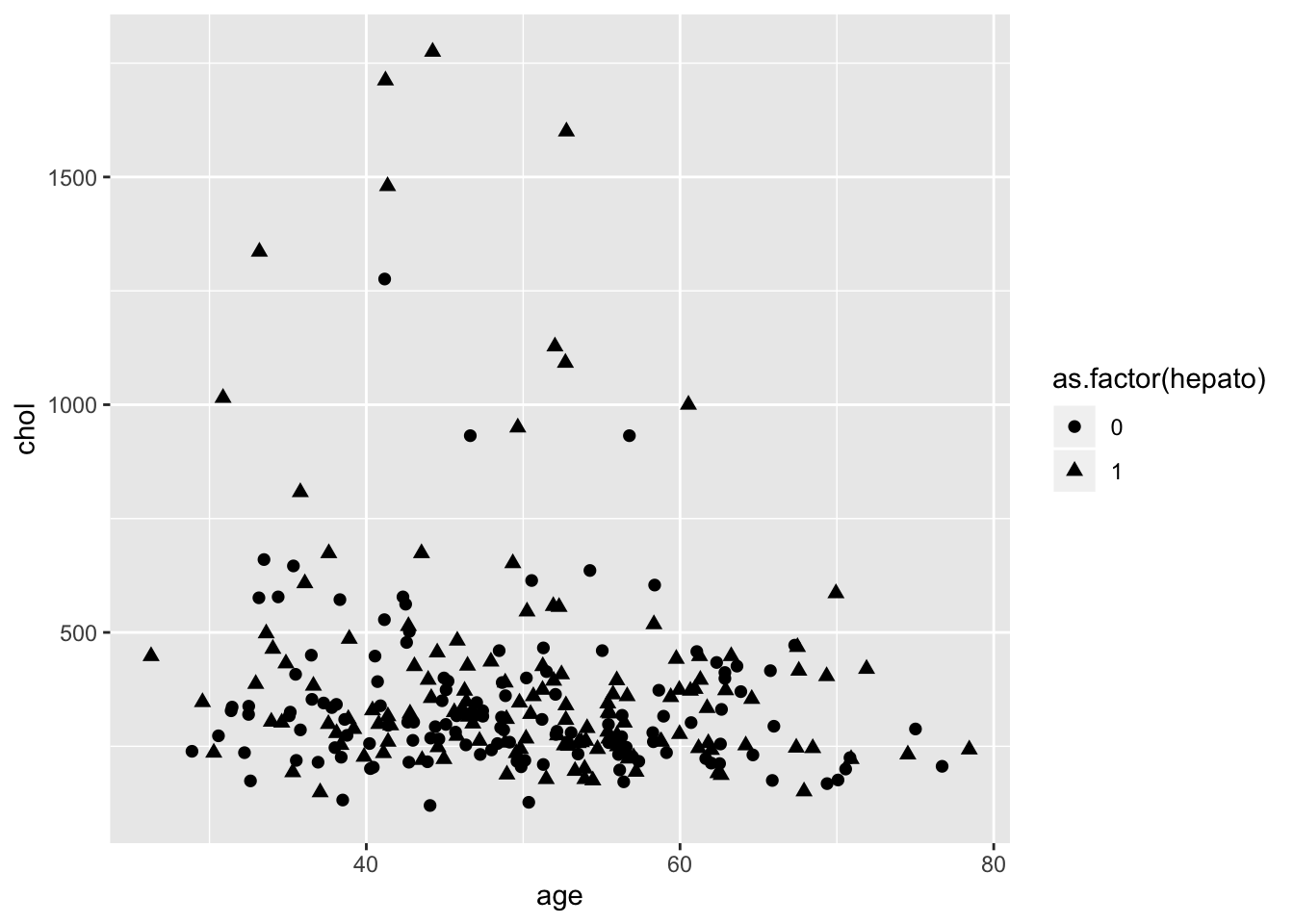

У использования цветов на графиков есть 3 основные функции:

• Для различения групп

• Для кодирования информации

• Для подчеркивания

Если на диаграмме рассеяния у нас есть и мэппинг формы, и мэппинг цвета, то победа будет за цветом, причем обычно с большим перевесом. Разные формы будут только отвлекать, поэтому и смысла в них особого не будет. Впрочем, при достаточно большом количестве точек даже при одинаковом цвете формы точек дадут какое-то представление только если эти точки довольно сильно обособляются в отдельные паттерны.

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 2,aes(shape = as.factor(hepato)))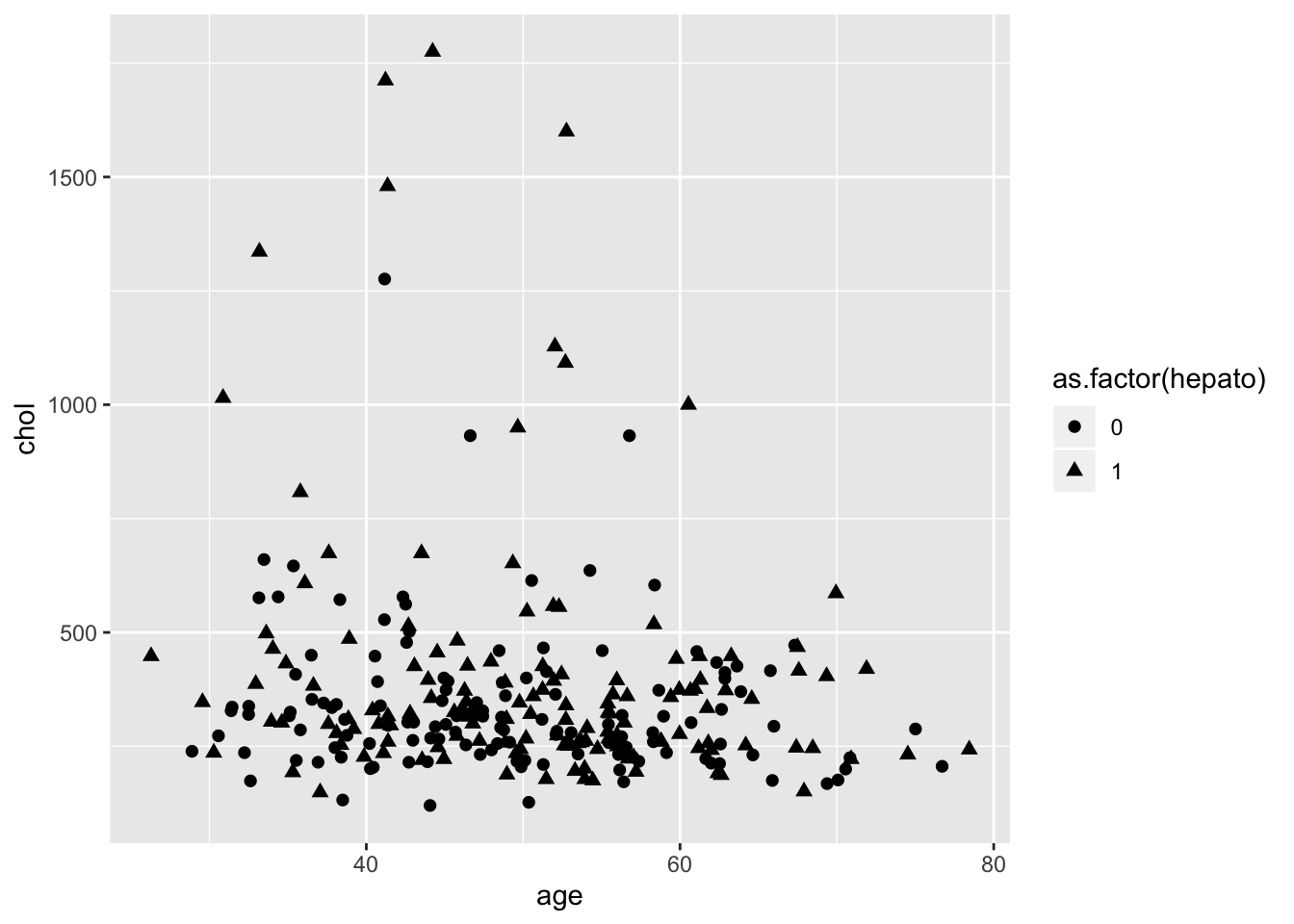

4.2.2.3.2 Overplotting и position

На картинке мы видим много точек, которые перекрывают друг друга. Мы не знаем, что стоит за точкой - возможно, под ней еще 10 таких же на той же позиции. Это плохо.

Данная проблема получила название оверплоттинга (overplotting). Решить ее можно разными способами.

Первый способ - добавить небольшой случайный шум (jitter). Это иногда подходит в случае дискретных значений - точки за счет шума немного “раздвигаются” и создают пятна большего или меньшего размера. Для зашумления можно использовать position adjustment:

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 2,aes(shape = as.factor(hepato)), position = "jitter")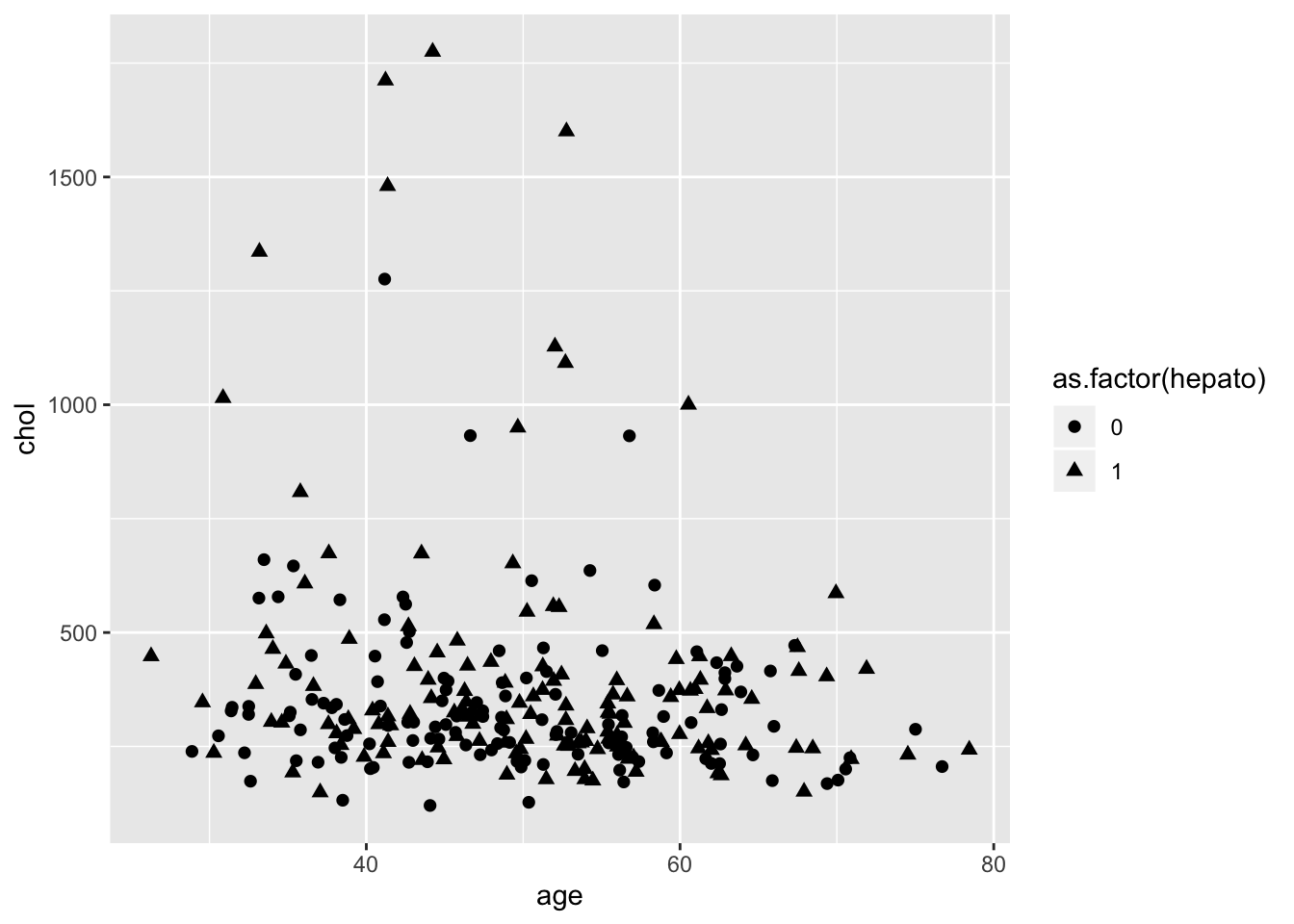

То же самое можно сделать выбрав geom_jitter - geom_point с position = "jitter" по умолчанию. Но это нам не подходит - у нас значения не дискретные и никакой разницы не видно. Поэтому мы решим проблему оверплоттинга с помощью использования прозрачных точек. Для этого есть параметр alpha =, который при 0 дает полностью прозрачные точки, а при 1 - полностью непрозрачные точки.

ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 2,aes(shape = as.factor(hepato)), alpha = 0.4)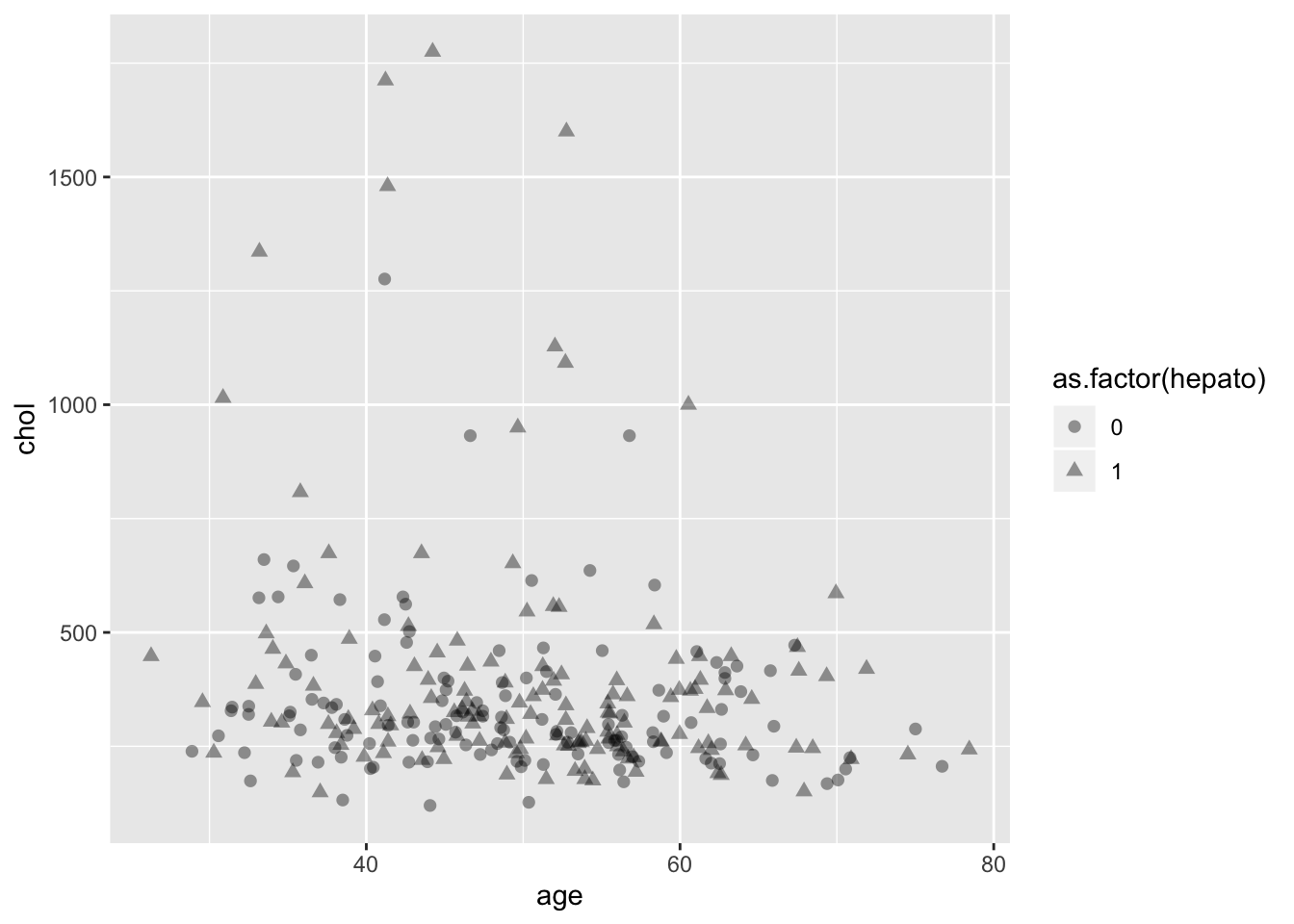

4.2.2.3.3 Двумерные гистограммы

Другой способ избежать оверплоттинга - использование других геомов, в которых можно кодировать плотность. Плотность здесь становится третьей переменной: мы разделяем все пространство на прямоугольники или шестиугольники, считаем сколько попало в каждый из них. Количество попаданий мы можем кодировать цветом. У нас получится “температурная карта” (heatmap) - там, где много точек, происходит что-то “горячее”, а там где их нет - что-то “холодное”. Но на самом деле, это всего лишь двумерная гистограмма.

В теории, мы могли бы сами агррегировать данные, использовать точки определенного цвета и размера и отрисовать двумерные гистограммы как точки или маленькие прямоугольники, просто в ggplot2 есть геомы, которые все это немного упрощают.

Для этого в ggplot2 есть несколько геомов: geom_hex(), geom_bin2d и их “трехмерные” братья (если плотность уже посчитана) - geom_raster(), geom_tile()

ggplot(pbcdt, aes(x = age, y = chol))+
  geom_hex()+
  scale_fill_viridis_c()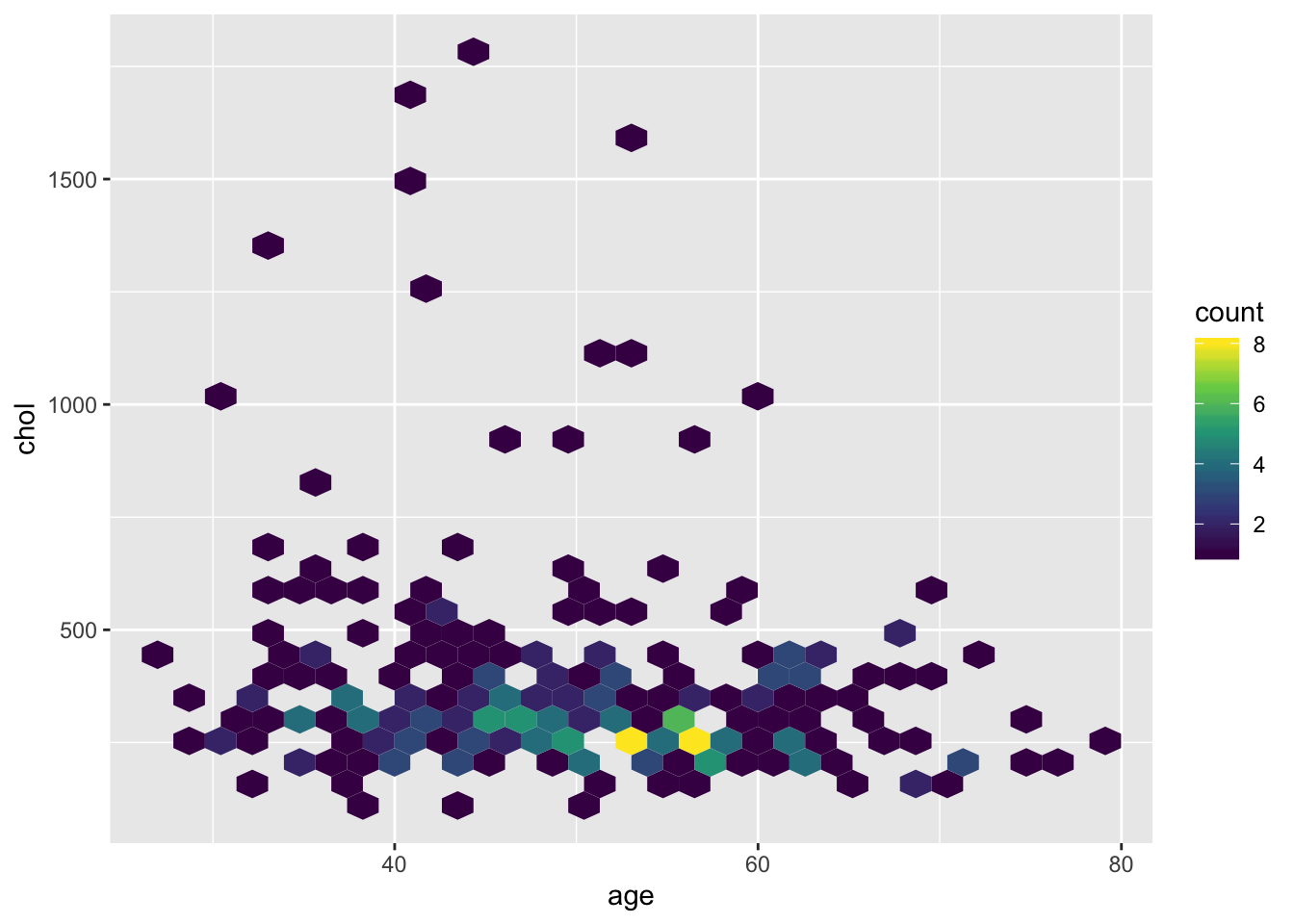

ggplot(pbcdt, aes(x = age, y = chol))+
  geom_bin2d(binwidth = c(1, 50))+
  scale_fill_viridis_c()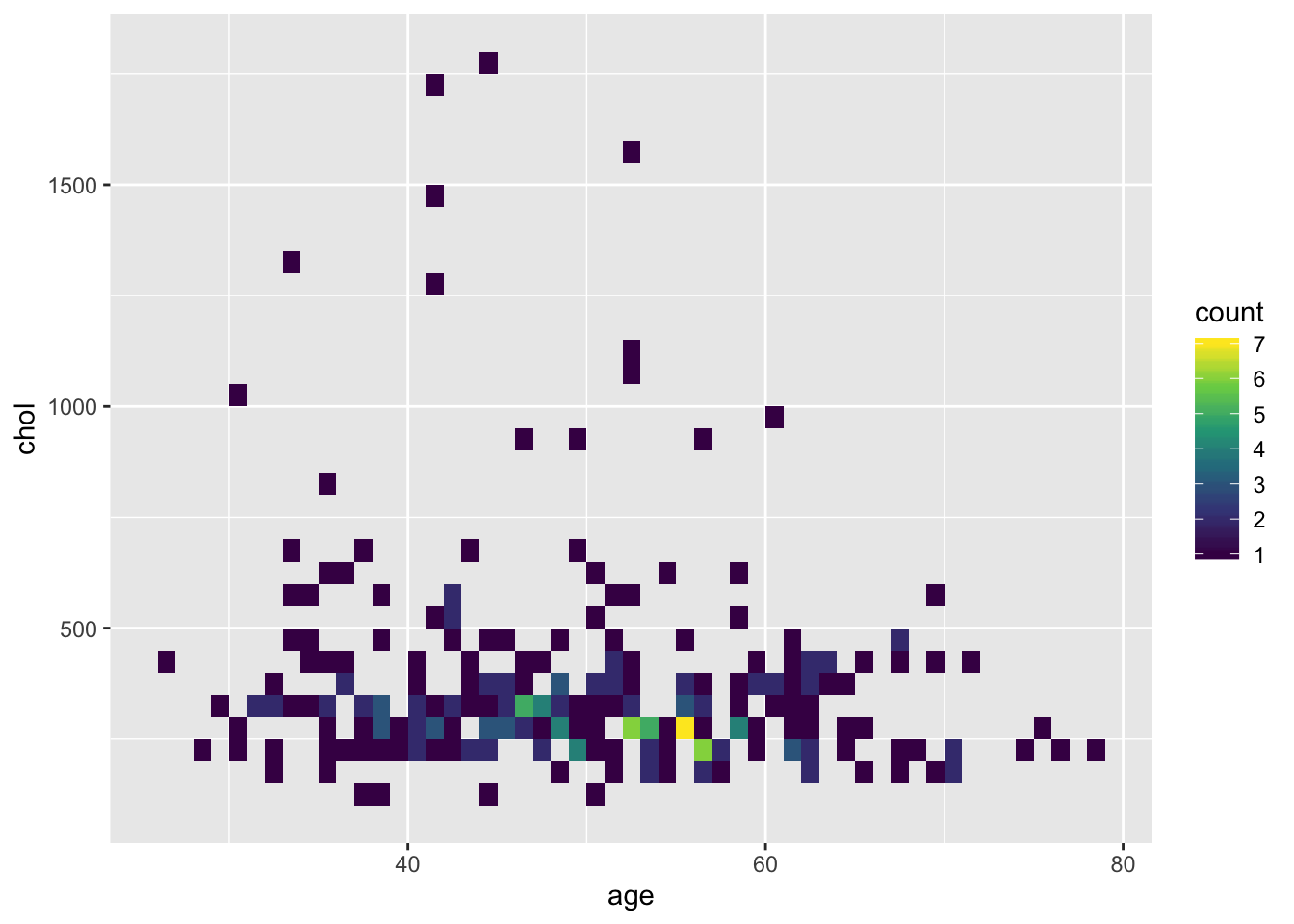

Геом geom_density_2d() позволяет нарисовать контуры плотности - довольно элегантный способ визуализировать пространственную динамику плотности. Можно

ggplot(pbcdt, aes(x = age, y = chol, colour = sex))+
  geom_density_2d()+
  geom_point(alpha = 0.4)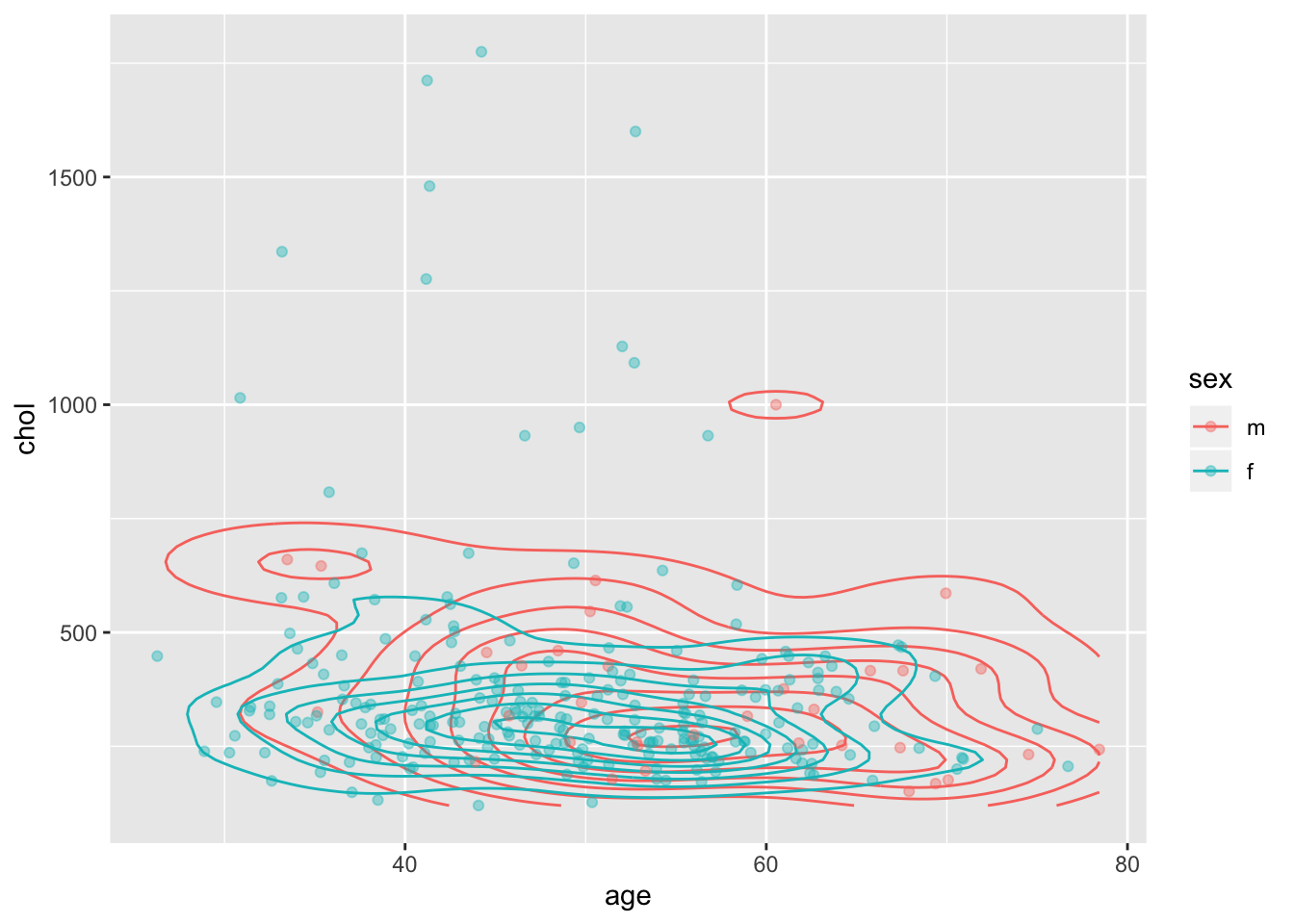

Мы можем наложить два слоя с разными геомами друг на друга. Таким образом можно создавать совершенно новые графики!

ggplot(pbcdt, aes(x = age, y = chol, colour = sex, fill = sex))+
   stat_density_2d(aes(alpha = ..level..), geom = "polygon")+
   geom_point(alpha = 0.4)+
   scale_alpha_continuous(range = c(0.01, 0.2))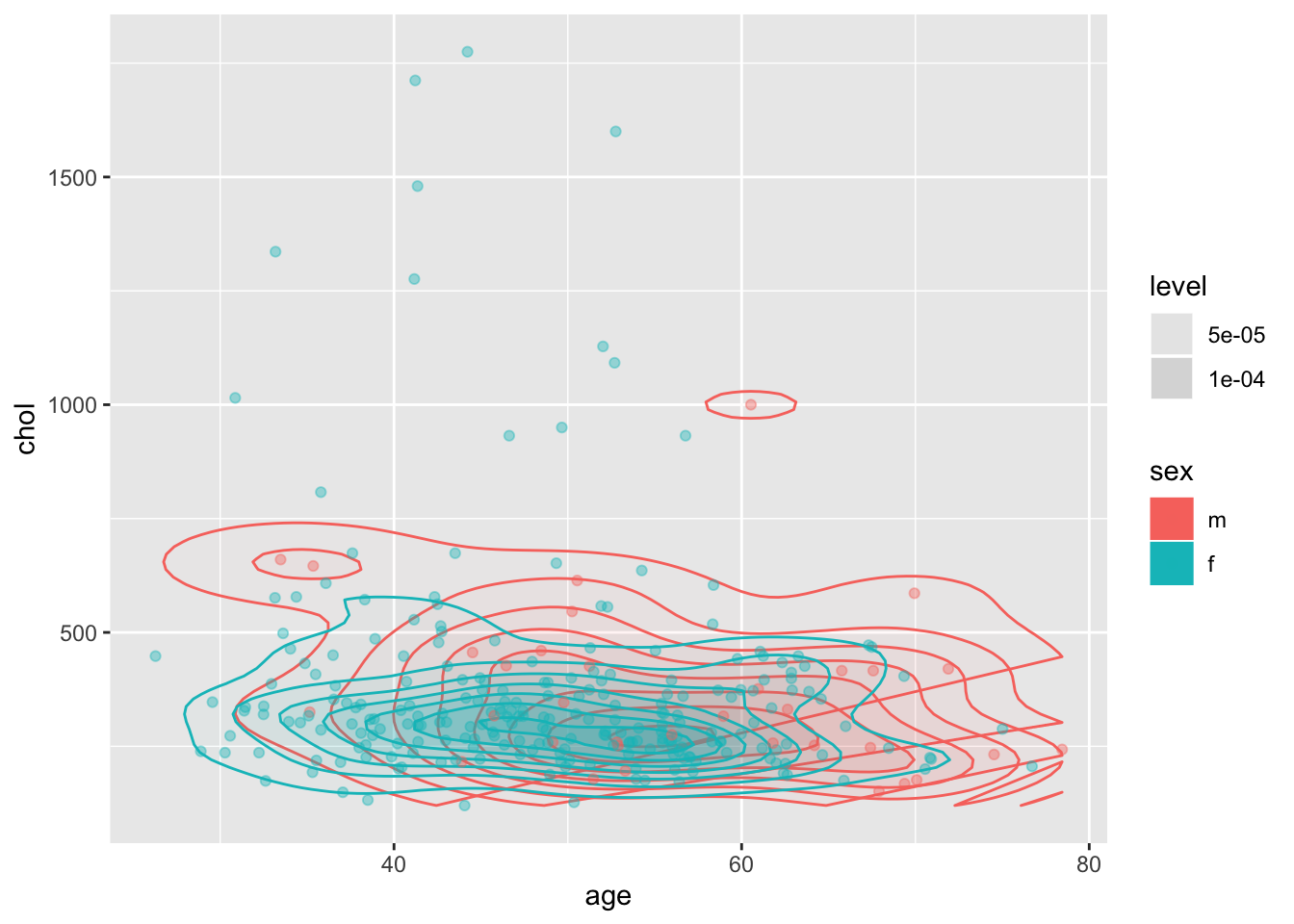

4.2.2.4 Пример 2: Столбиковая диаграмма

ggplot(pbcdt)+
  geom_bar(aes(x = sex, fill = sex))+
  facet_grid(rows = vars(stage), cols = vars(hepato))+
  coord_flip()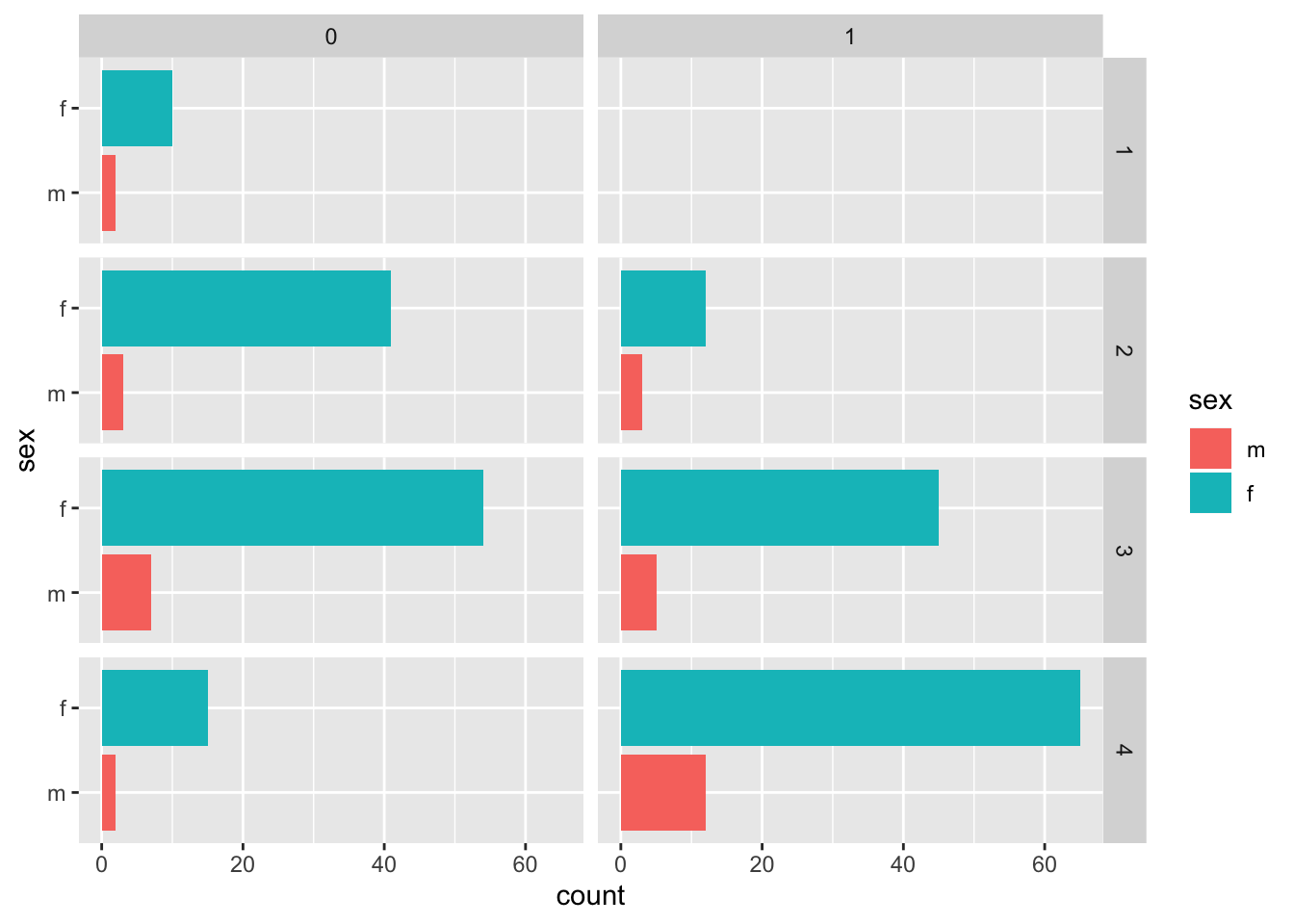

4.2.2.5 Пример 3: Гистограмма и ящик с усами

ggplot(pbcdt, aes(x = chol, fill = as.factor(stage)))+
  geom_histogram(position = "identity")+
  facet_grid(rows = vars(stage))

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.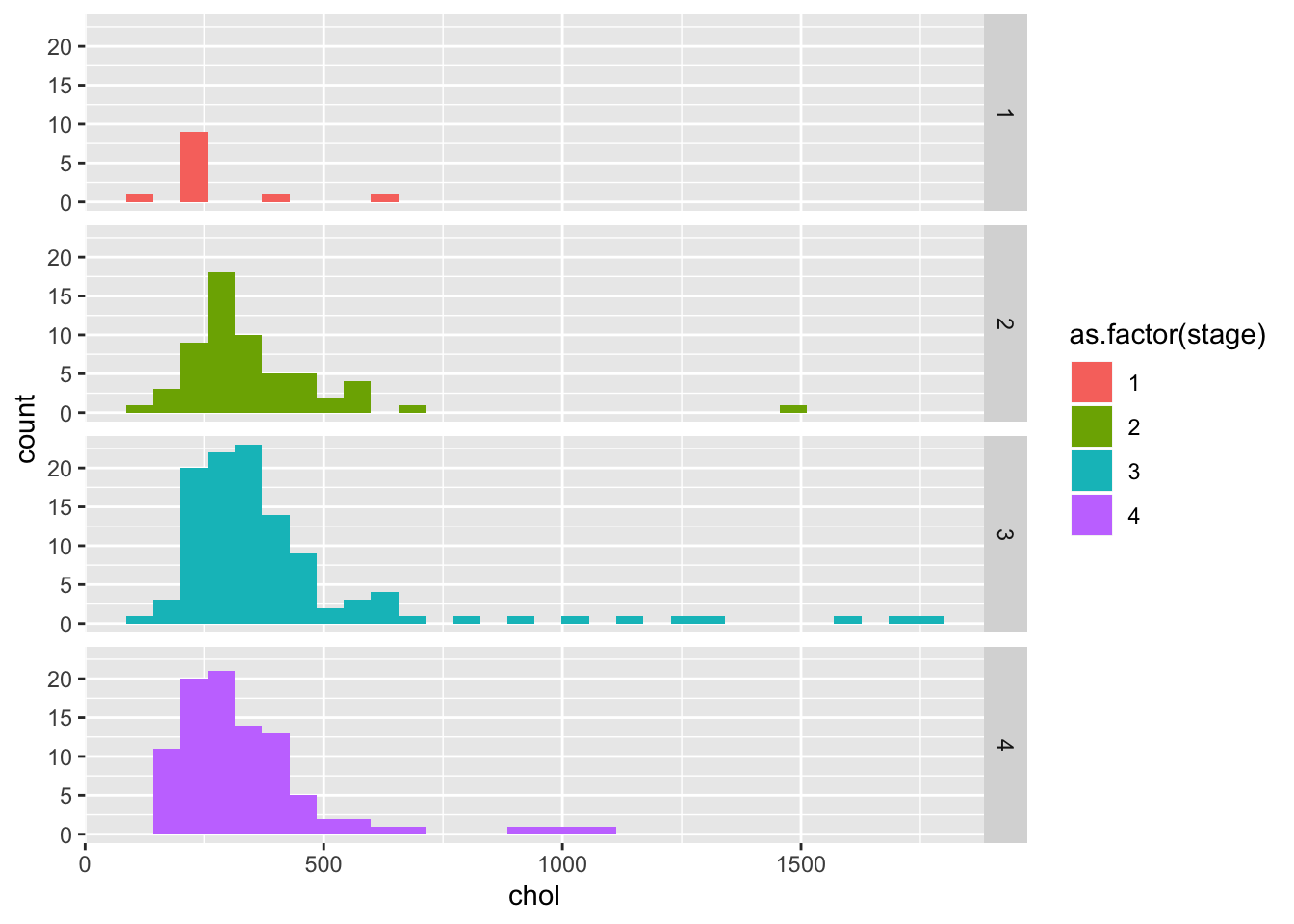

ggplot(pbcdt, aes(x = chol, fill = as.factor(stage)))+
  geom_density(position = "identity")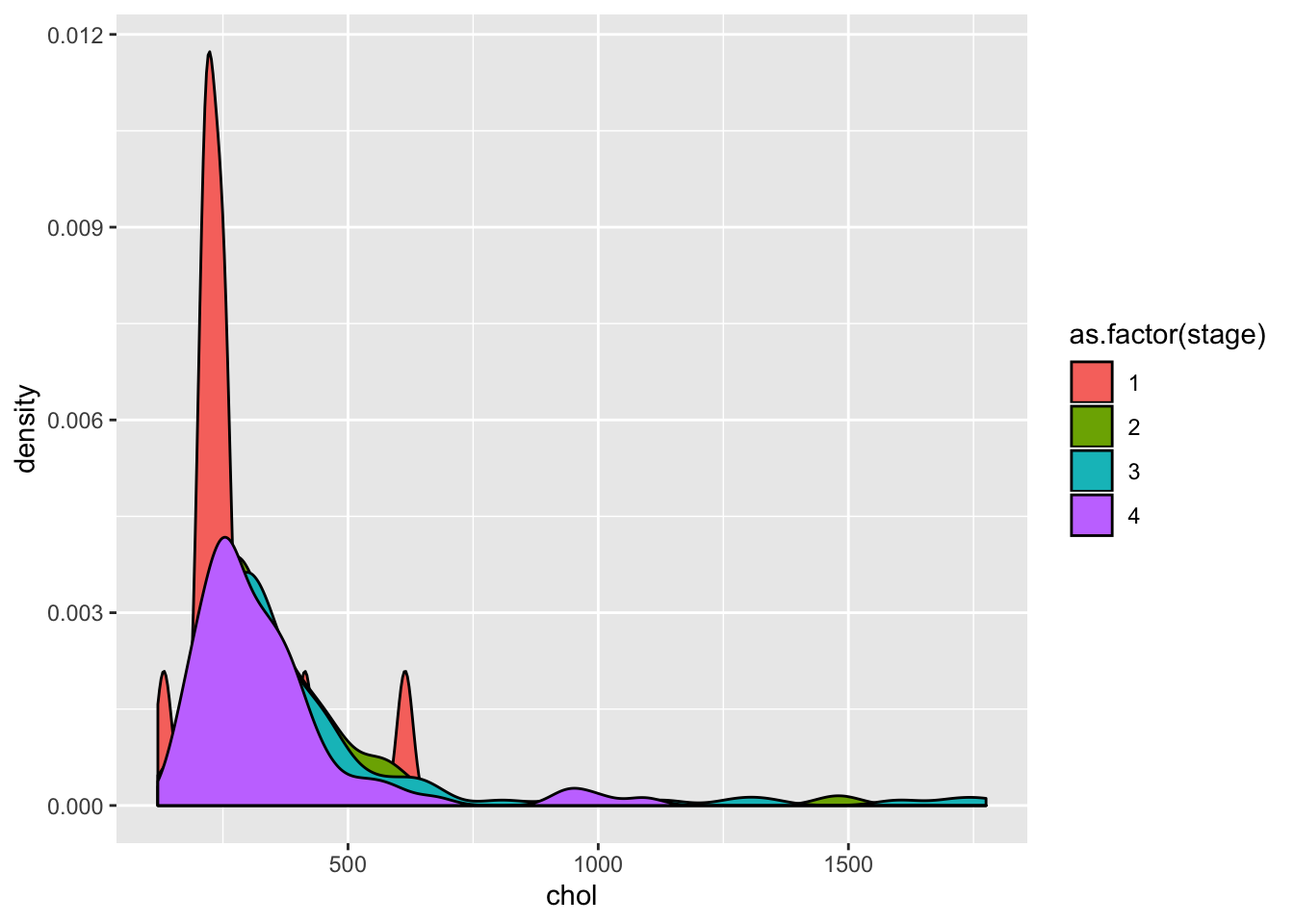

ggplot(pbcdt, aes(x = chol, fill = as.factor(stage)))+
  geom_density(position = "identity", alpha = 0.4, adjust = 3)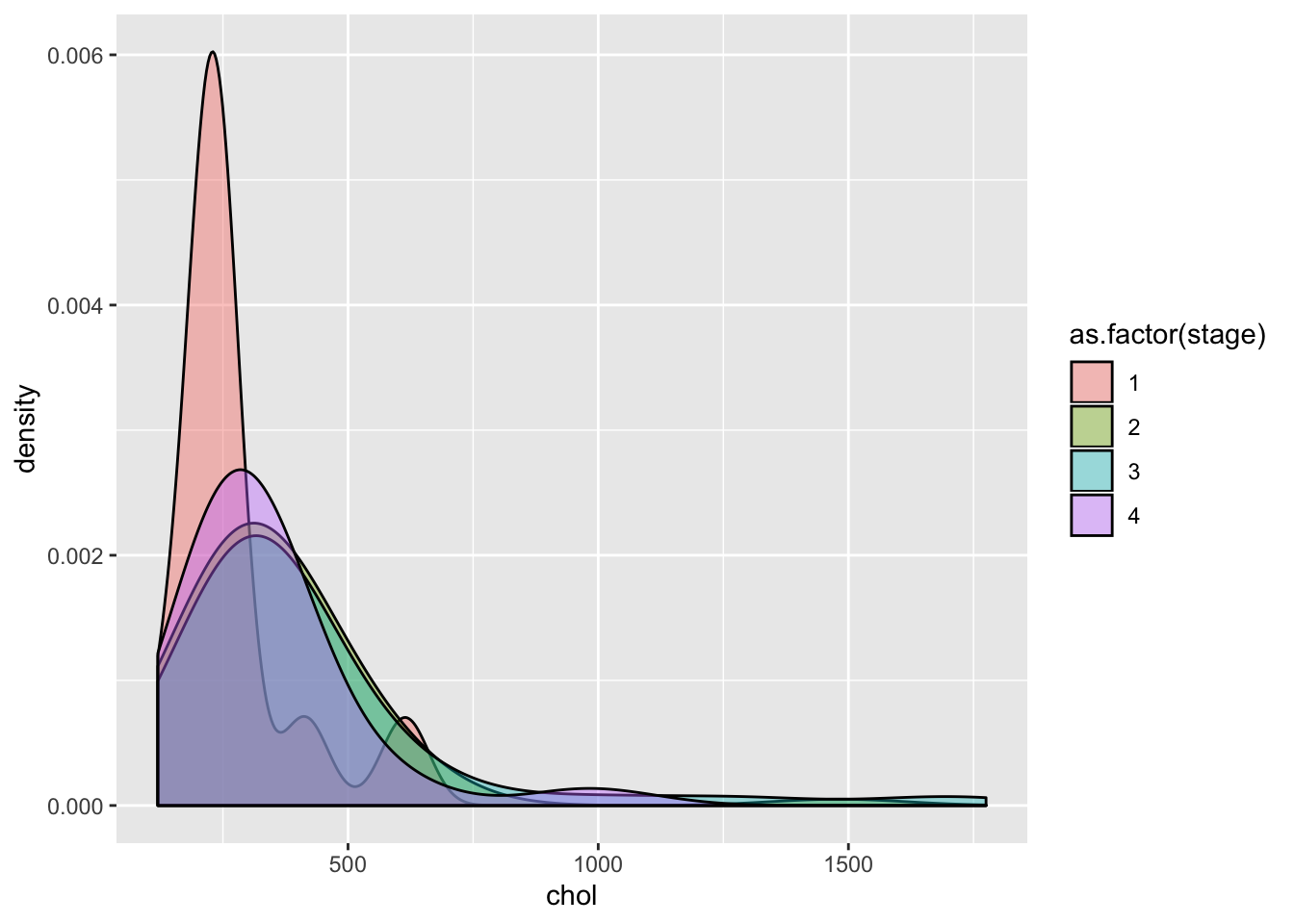

ggplot(pbcdt, aes(x = as.factor(stage), y = chol, fill = as.factor(stage)))+
  geom_violin()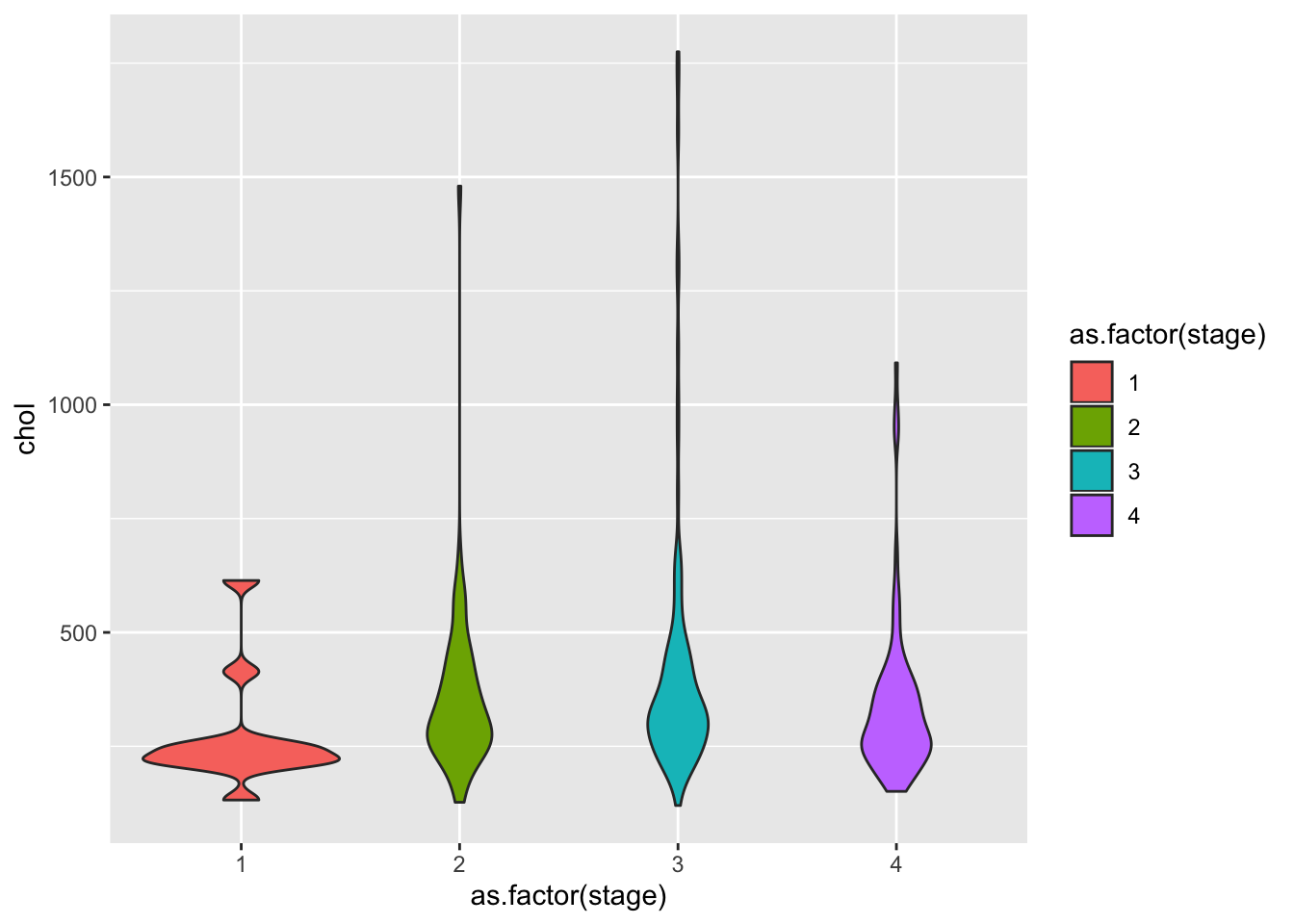

ggplot(pbcdt, aes(x = as.factor(stage), y = chol))+
  geom_boxplot()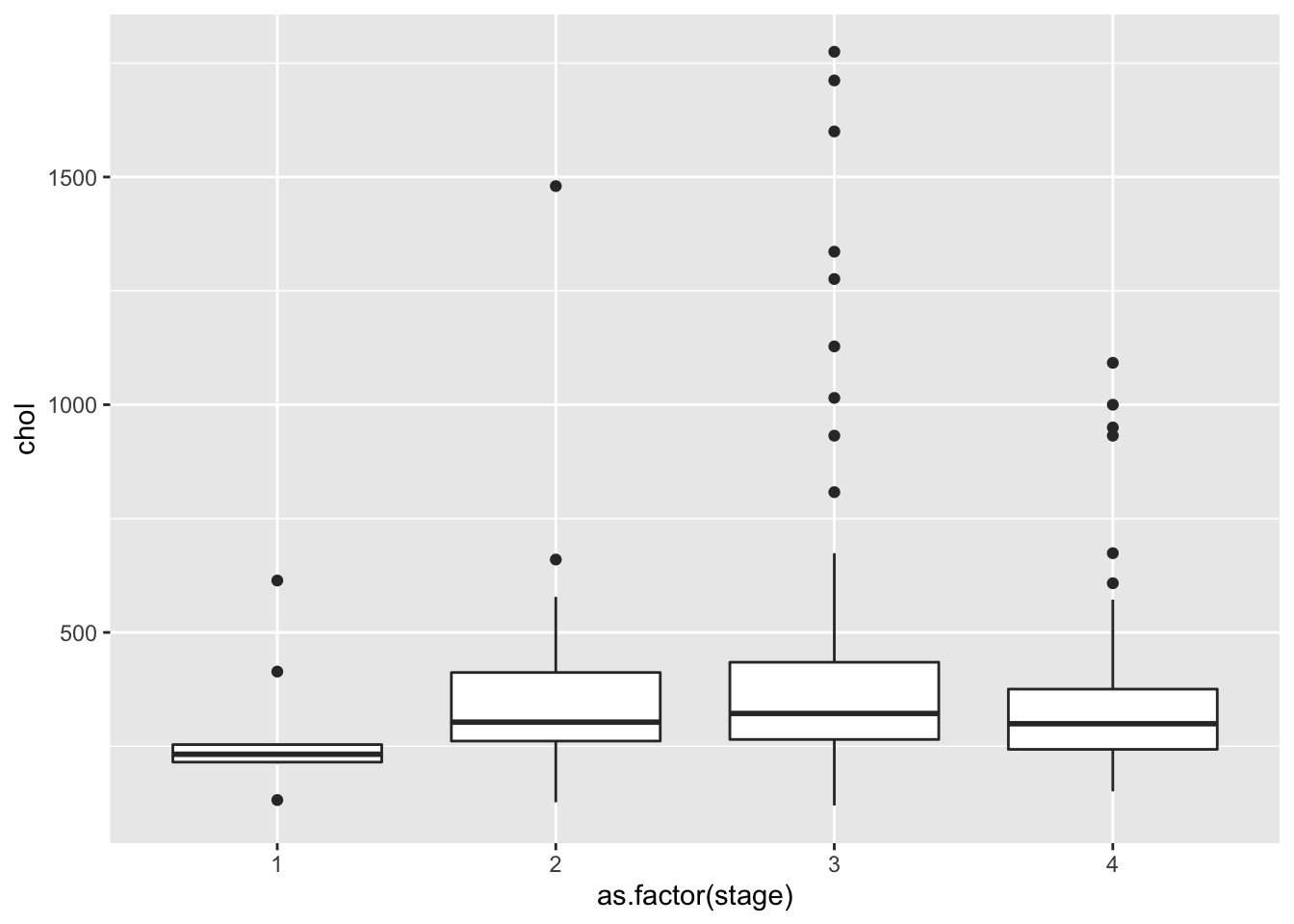

ggplot(pbcdt, aes(x = as.factor(stage), y = chol))+
  geom_violin(aes(fill = as.factor(stage)))+
  geom_boxplot(width = 0.1)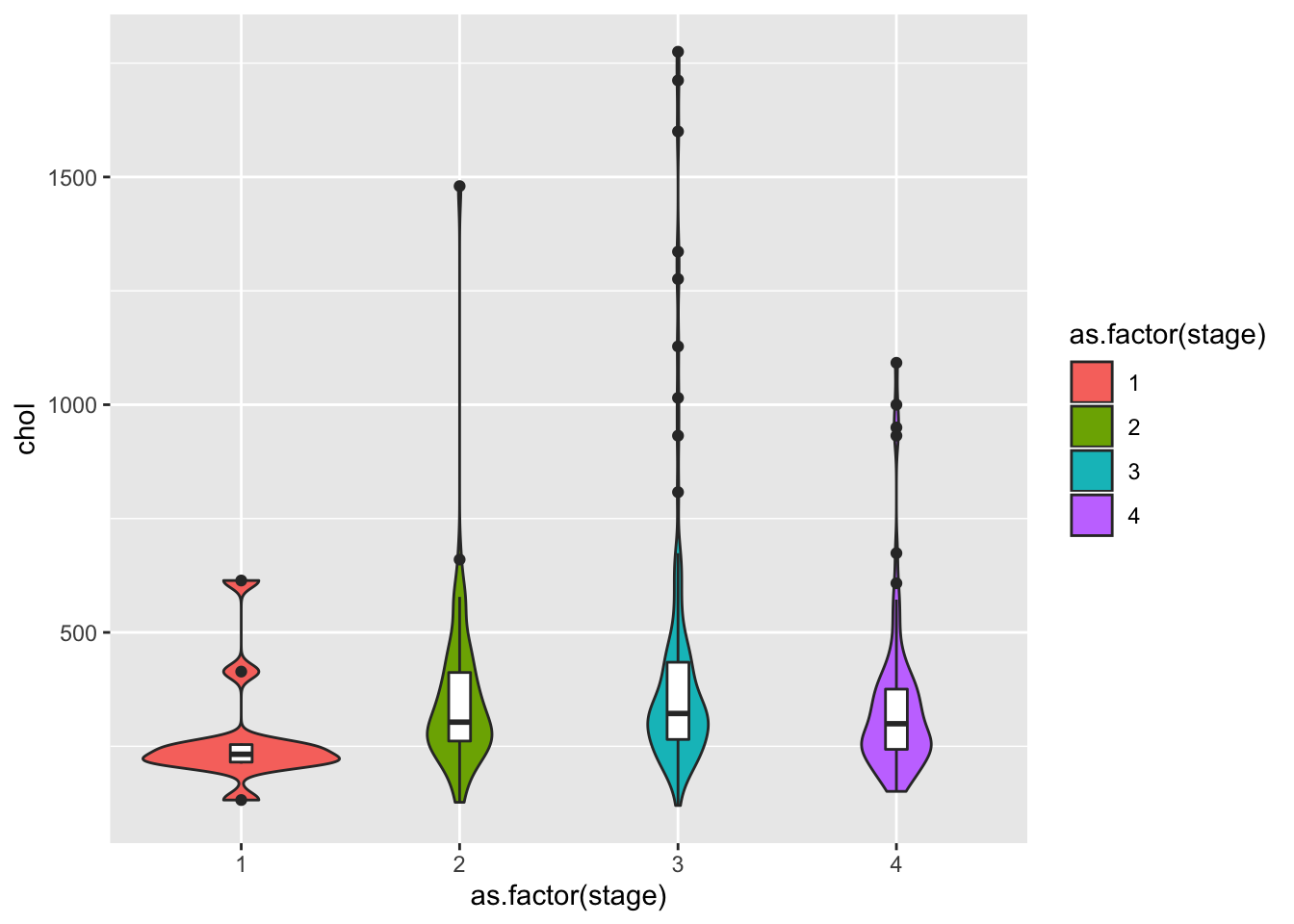

4.2.3 Дополнения к ggplot2

ggplot2 стал настолько популярным пакетом, что существуют сторонние пакеты, которые расширяют его функциональность. В некоторых можно найти новые геомы, в некоторых - новые темы и палитры. Ознакомиться с разнообразием расширений ggplot2 можно здесь. Мы же остановимся на одном из них - cowplot

4.2.4 cowplot

Для начала нужно установить cowplot:

install.packages("cowplot")

И подгрузить его:

library(cowplot)

g1 <- ggplot(data = pbcdt, mapping = aes(x = age, y = chol))+
  geom_point(size = 2,aes(colour = sex), alpha = 0.3)

g2 <- ggplot(pbcdt, aes(x = age, y = chol))+
  geom_hex()+
  scale_fill_viridis_c()

g3 <- ggplot(pbcdt, aes(x = age, y = chol))+
  geom_hex()+
  scale_fill_viridis_c()

g4 <- ggplot(pbcdt, aes(x = age, y = chol, colour = sex))+
  geom_density_2d()+
  geom_point(alpha = 0.1)

plot_grid(g1, g4,g2, g3, labels = LETTERS[1:4])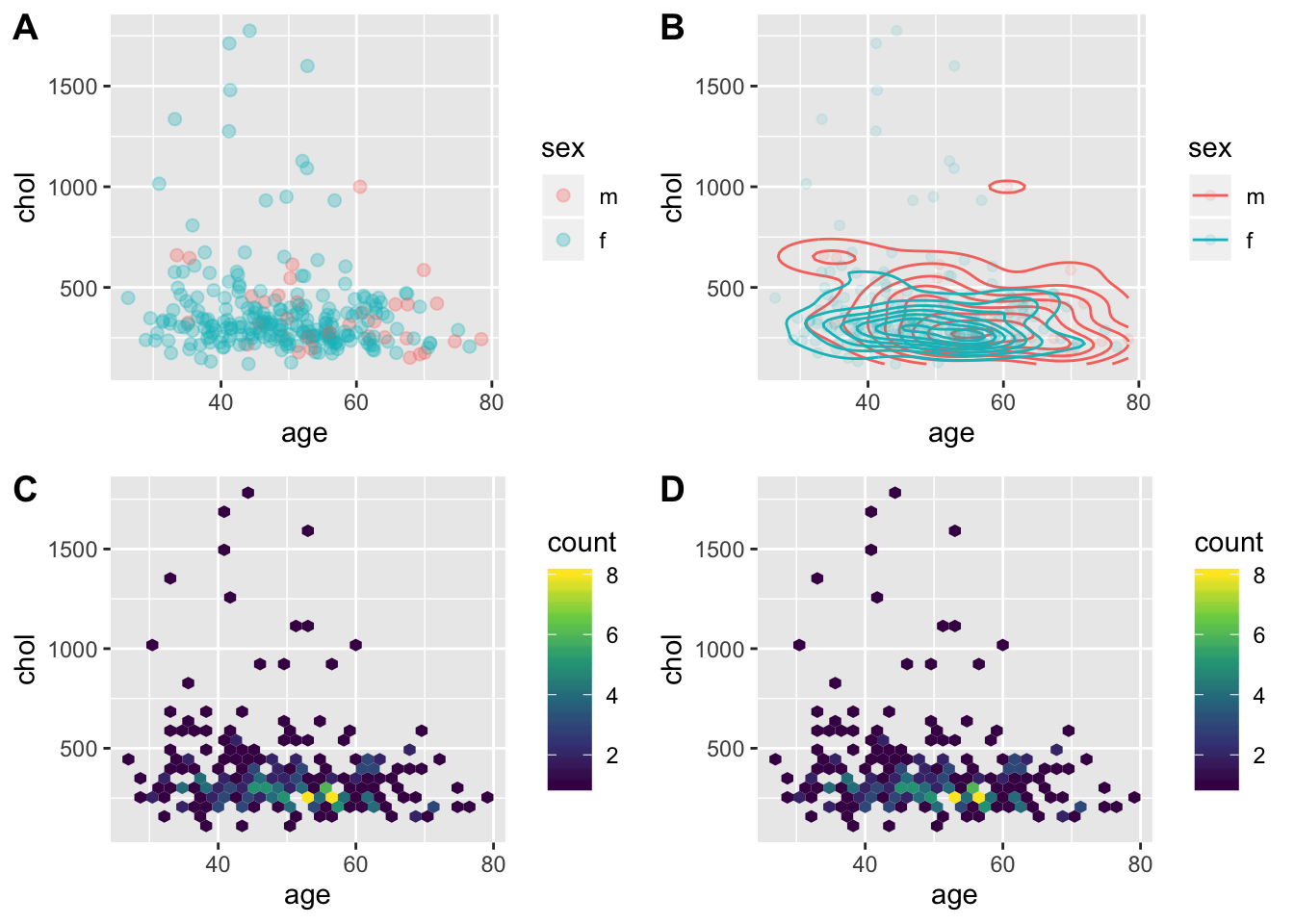

Если хотите вернуть стандартную тему ggplot2, то выполните следующую команду:

theme_set(theme_grey())

4.2.5 plotly

install.packages("plotly")

library(plotly)

ggplotly(g1)

---

7. Квартиль — это частный пример квантиля. Другой известный квантиль — процентиль. Процентили часто используют для сравнения значения с другими значениями. Например, 63ий процентиль означает, что данное значение больше 63% значений в выборке.↩