17 Общая линейная модель и ее расширения

17.1 Общая линейная модель

Обобщением множественной линейной регрессии можно считать общую линейную модель (general linear model). Общая линейная модель может предсказывать не одну, а сразу несколько объясняемых переменных в отличие от множественной линейной регрессии.

\[Y = XB\] где \(Y\) — матрица объясняемых переменных, \(X\) — матрица предикторов, \(B\) — матрица параметров.

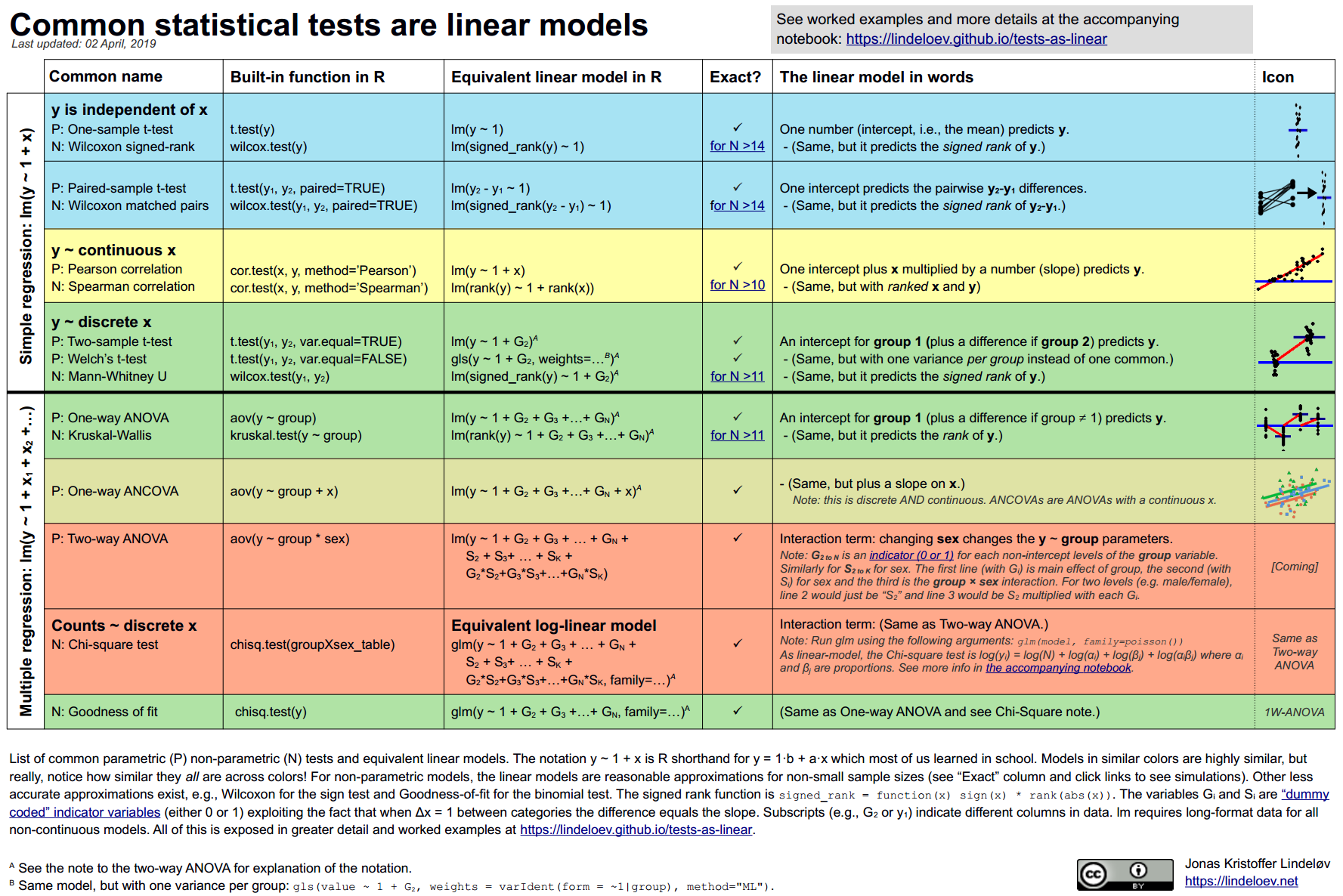
Почти все пройденные нами методы можно рассматривать как частный случай общей линейной модели: t-тесты, коэффициент корреляции Пирсона, линейная регрессия, ANOVA.

17.2 Обобщенная линейная модель

Обобщенная линейная модель (generalized linear model) была придумана как обобщение линейной регрессии и ее сородичей: логистической регрессии и пуассоновской регрессии.

Общая линейная модель задается формулой \[Y = XB\]

Обобщенная оборачивает предиктор \(XB\) связывающей функцией (link function), которая различается для разных типов регрессионных моделей.

Давайте попробуем построить модель, в которой объясняемой переменной будет то, является ли супергерой хорошим или плохим.

heroes$good <- heroes$Alignment == "good"

Обычная линейная модель нам не подходит, если распределение наших ошибок далеко от нормального. А это значит, что мы не можем использовать общую линейную модель с бинарной объясняемой переменной. Эту проблему решает логистическая регрессия, которая является частным случаем обобщенной линейной модели.

Для этого нам понадобится функция glm(), а не lm() как раньше. Ее синтаксис очень похож, но нам теперь нужно задать еще один важный параметр family = для выбора связывающей функции (в данном случае это логит-функция, которая является связующей функцией по умолчанию для биномиального семейства функций в glm()).

heroes_good_glm <- glm(good ~ Weight + Gender, heroes, family = binomial()) 
summary(heroes_good_glm)

## 
## Call:
## glm(formula = good ~ Weight + Gender, family = binomial(), data = heroes)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.8674  -1.3103   0.6334   0.9155   2.4007  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  1.763917   0.235410   7.493 6.73e-14 ***
## Weight      -0.004253   0.001124  -3.783 0.000155 ***
## GenderMale  -0.760310   0.245851  -3.093 0.001984 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 605.22  on 477  degrees of freedom
## Residual deviance: 570.88  on 475  degrees of freedom
##   (256 observations deleted due to missingness)
## AIC: 576.88
## 
## Number of Fisher Scoring iterations: 4

Результат очень похож по своей структуре на glm(), однако вместо \(R^2\) перед нами AIC. AIC расшифровывается как информационный критерий Акаике (Akaike information criterion) — это критерий использующийся для выбора из нескольких моделей. Чем он меньше, тем лучше модель. Как и Adjusted R², AIC “наказывает” за большое количество параметров в модели.

Поскольку AIC — это относительный показатель качества модели, нам нужно сравнить его с AIC другой, более общей модели. Можно сравнить с моделью без веса супергероев.

heroes_good_glm_noweight <- glm(good ~ Gender, heroes, family = binomial()) 
summary(heroes_good_glm_noweight)

## 
## Call:
## glm(formula = good ~ Gender, family = binomial(), data = heroes)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.8082  -1.4164   0.6586   0.9559   0.9559  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   1.4178     0.1785   7.944 1.95e-15 ***
## GenderMale   -0.8716     0.2012  -4.332 1.48e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 873.81  on 698  degrees of freedom
## Residual deviance: 853.24  on 697  degrees of freedom
##   (35 observations deleted due to missingness)
## AIC: 857.24
## 
## Number of Fisher Scoring iterations: 4

AIC стал больше, следовательно, мы выберем модель с весом супергероев.

17.3 Модель со смешанными эффектами

Модели со смешанными эффектами (mixed-effects models) — это то же самое, что и иерархическая регрессия (hierarchical regression) или многоуровневое моделирование (multilevel modelling). Этому методу повезло иметь много названий - в зависимости от области, в которой он используется. Модели со смешанными эффектами позволяет включать в линейную регрессию не только фиксированные эффекты (fixed effects), но и случайные эффекты (random effects).

Для экспериментальных дисциплин это интересно тем, что в таких моделях можно не усреднять показатели по испытуемым или образцам, а учитывать влияние соотвествующей группирующей переменной как случайный эффект. В отличие от обычного фактора как в линейной регрессии или дисперсионном анализе (здесь он называется фиксированным), случайный эффект не интересует нас сам по себе, а его значения считаются случайной переменной.

Смешанные модели используются в самых разных областях. Они позволяют решить проблему зависимости наблюдений без усреднения значений по испытуемым или группам, что повышает статистическую мощность.

Для работы со смешанными моделями в R есть два известных пакета: nlme и более современный lme4.

install.packages("lme4")

library(lme4)

Для примера возьмем данные исследования влияния депривации сна на время реакции.

data("sleepstudy")

Данные представлены в длинном формате: каждая строчка — это усредненное время реакции для одного испытуемого в соответствующий день эксперимента.

sleepstudy %>%
  ggplot(aes(x = Days, y = Reaction)) +
  geom_line() +
  geom_point() +
  scale_x_continuous(breaks = 0:9) +
  facet_wrap(~Subject) +
  theme_minimal()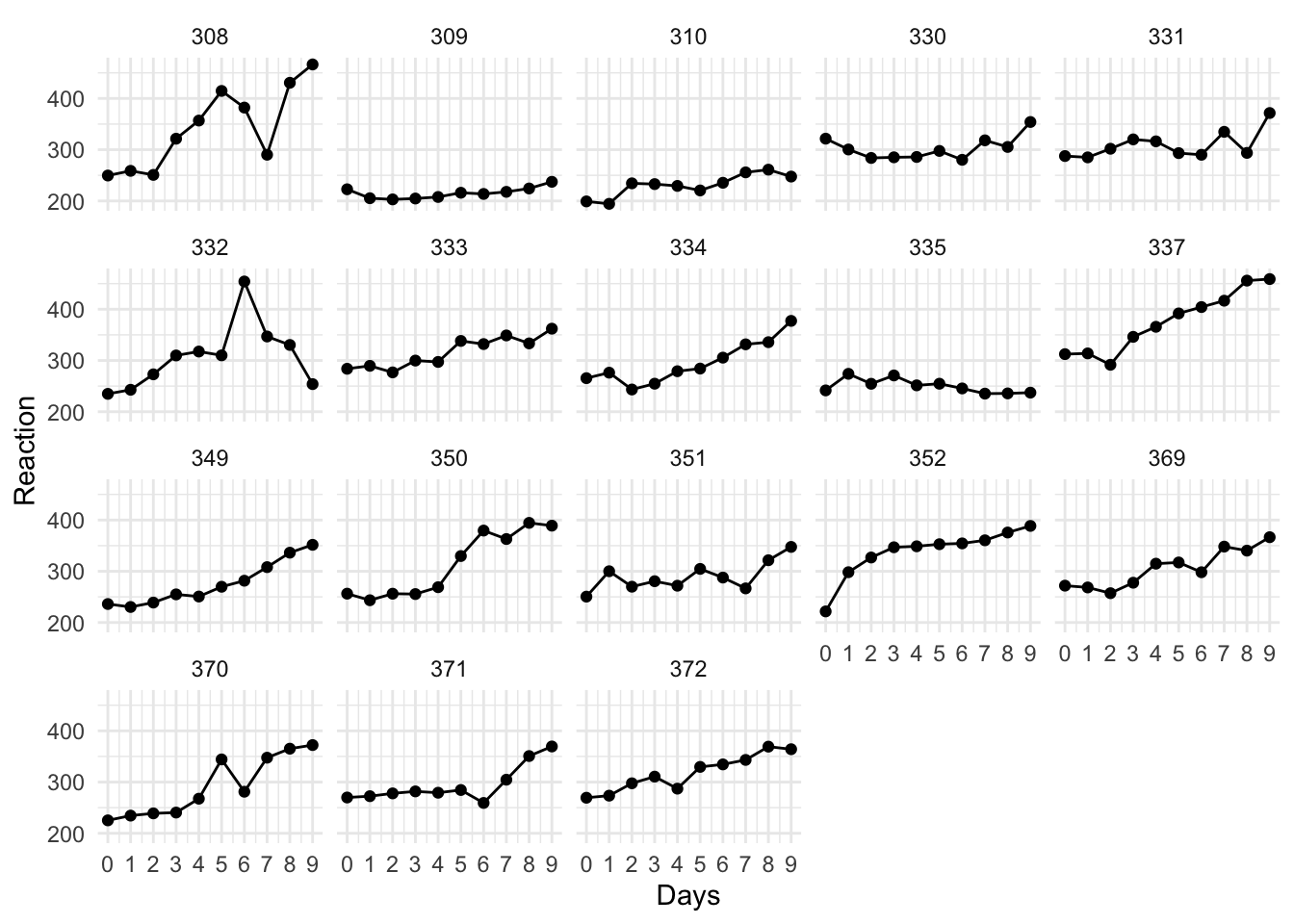

Можно заметить, что, в среднем, время реакции у испытуемых повышается от первого к последнему дню. С помощью смешанных моделей мы можем проверить, различается ли скорость возрастания времени реакции от дня к дню у разных испытуемых.

Для этого мы сравниваем две модели, одна из которых является “вложенной” в другую, то есть усложненной версией более общей модели. В данном случае, более общая модель предполагает, что время реакции увеличивается у всех испытуемых одинаково, а испытуемые различаются только средним временем реакции.

sleep_lme0 <- lmer(Reaction ~ Days + (1 | Subject), sleepstudy)
sleep_lme1 <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)

Визуализируем предсказания двух моделей:

sleepstudy$predicted_by_sleep_lme0 <- predict(sleep_lme0)
sleepstudy$predicted_by_sleep_lme1 <- predict(sleep_lme1)

sleepstudy %>%
  rename(observed_reaction_time = Reaction) %>%
  pivot_longer(cols = c(observed_reaction_time, predicted_by_sleep_lme0, predicted_by_sleep_lme1), names_to = "model", values_to = "Reaction") %>%
  ggplot(aes(x = Days, y = Reaction)) +
  geom_line(aes(colour = model)) +
  #geom_line(aes(y = predicted_by_M1), colour = "orange") + 
  #geom_line(aes(y = predicted_by_M2), colour = "purple") +   
  geom_point(data = sleepstudy, alpha = 0.4) +
  scale_x_continuous(breaks = 0:9) +
  facet_wrap(~Subject) +
  theme_minimal()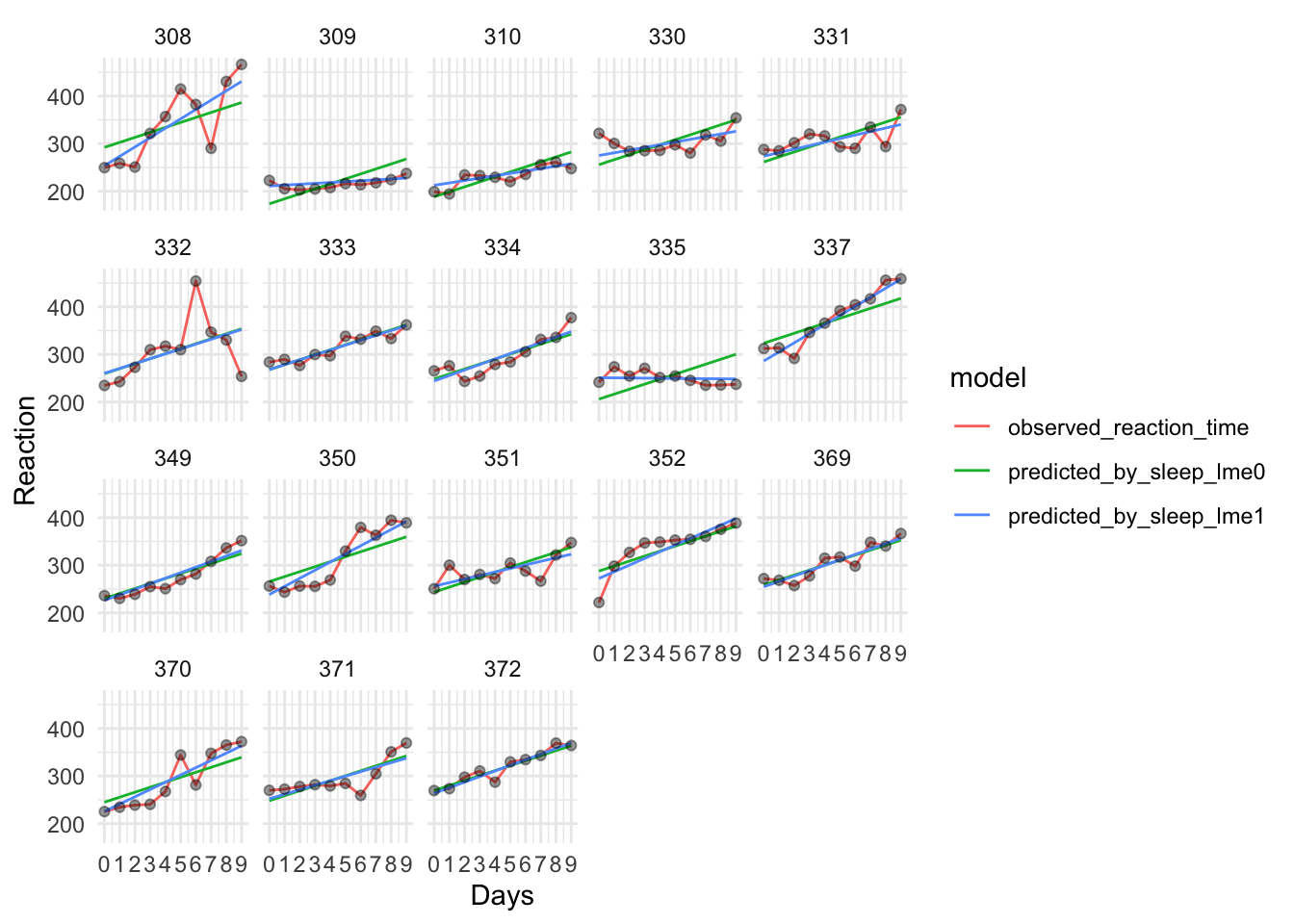

Зеленая линия (нулевая модель) имеет везде один и тот же наклон, а синяя (альтернативная модель) имеет разный наклон у всех испытуемых.

Есть несколько способов сравнивать модели, например, уже знакомый нам AIC. Кроме того, можно сравнить две модели с помощью теста хи-квадрат, восполльзовавшись функцией anova().

anova(sleep_lme0, sleep_lme1)

Модель со случайным наклоном прямой оказалась лучше, о чем нам говорят как более низкие AIC и BIC, так и тестирование с помощью хи-квадрат.