20 Решения заданий

You can omit tasks with asterisks (*): these are the tasks of higher difficulty, so you need to think a lot on them, not just apply tools you’ve just learned.

20.1 Intro to R

Divide 9801 by 9.

9801/9

## [1] 1089

Calculate logarithm of 2176782336 with base 6.

log(2176782336, 6)

## [1] 12

Calculate natural logarithm of 10 and multiply it by 5.

log(10)*5

## [1] 11.51293

Using function sin() calculate \(\sin (\pi), \sin \left(\frac{\pi}{2}\right), \sin \left(\frac{\pi}{6}\right)\).

The value of \(\pi\) is a predefined constant in R (pi).

sin(pi)

## [1] 1.224647e-16

sin(pi/2)

## [1] 1

sin(pi/6)

## [1] 0.5

20.2 Vectors creation

Create a vector with values 2, 30 and 4000.

c(2, 30, 4000)

## [1]    2   30 4000

Create a vector from 1 to 20.

1:20

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Create a vector from 20 to 1.

20:1

##  [1] 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1

Function sum() returns sum of all elements in input. Calculate sum of the first 100 natural numbers (i.e. all whole numbers from 1 to 100).

sum(1:100)

## [1] 5050

Create a vector from 1 to 20 and then back to 1. Number 20 must appear only once!

c(1:20, 19:1)

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 19 18 17 16 15
## [26] 14 13 12 11 10  9  8  7  6  5  4  3  2  1

Create a vector with values 5, 4, 3, 2, 2, 3, 4, 5:

c(5:2, 2:5)

## [1] 5 4 3 2 2 3 4 5

Create a vector 2, 4, 6, … , 18, 20.

seq(2, 20, 2)

##  [1]  2  4  6  8 10 12 14 16 18 20

Create a vector 0.1, 0.2, 0.3, …, 0.9, 1.

seq(0.1, 1, 0.1)

##  [1] 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

2020 year is a leap year. The next leap year will be 4 years later — it will be year 2024. Create a calendar of all leap years for the XXI century since year 2020.

2100 year belongs to the XXI century, not the XXII.

seq(2020, 2100, 4)

##  [1] 2020 2024 2028 2032 2036 2040 2044 2048 2052 2056 2060 2064 2068 2072 2076
## [16] 2080 2084 2088 2092 2096 2100

Create a vector containing 20 repetitions of “Hey!”

rep("Hey!", 20)

##  [1] "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!"
## [11] "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!" "Hey!"

As I said, many functions that work with scalars (one value), also work well with vectors that contain more than one value. Try to calculate square root of numbers from 1 to 10 using function sqrt() and svae the result in a variable roots.

roots <- sqrt(1:10)
roots

##  [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751 2.828427
##  [9] 3.000000 3.162278

Let’s check that it is really square roots by calculating the 2nd degree of all values of roots!

roots ^ 2

##  [1]  1  2  3  4  5  6  7  8  9 10

If everything is correct you can get the same result by multiplying the roots by itself.

roots * roots

##  [1]  1  2  3  4  5  6  7  8  9 10

- Create a vector with one 1, two 2, three 3, … , nine 9.

rep(1:9, 1:9)

##  [1] 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 9 9
## [39] 9 9 9 9 9 9 9

20.3 Coercion

Create a vector vec1 that combines 3 and values "My" and "vector".

vec1 <- c(3, "My", "vector")
vec1

## [1] "3"      "My"     "vector"

Try to substitute TRUE from 10. What happens and why?

10 - TRUE

## [1] 9

Combine values 10 and TRUE in a vector vec2.

vec2 <- c(10, TRUE)
vec2

## [1] 10  1

Combine vector vec2 and value "r":

c(vec2, "r")

## [1] "10" "1"  "r"

Combine values 10, TRUE, "r" to a vector.

c(10, TRUE, "r")

## [1] "10"   "TRUE" "r"

20.4 Vectorisation

Create a vector p with values 4, 5, 6, 7, and vector q, with values 0, 1, 2, 3.

p <- 4:7
p

## [1] 4 5 6 7

q <- 0:3
q

## [1] 0 1 2 3

Calculate element-wise sum of p and q:

p + q

## [1]  4  6  8 10

Calculate element-wise difference of p and q:

p - q

## [1] 4 4 4 4

Divide all values of p by corresponding value of q:

Yep, you will divide by 0!

p / q

## [1]      Inf 5.000000 3.000000 2.333333

Raise each value of p to the corresponding power from q.

p ^ q

## [1]   1   5  36 343

Multiply each value of p by 10

p * 10

## [1] 40 50 60 70

Create a vector of squares for numbers from 1 to 10:

(1:10)^2

##  [1]   1   4   9  16  25  36  49  64  81 100

Create a vector with values 0, 2, 0, 4, … , 18, 0, 20.

1:20 * 0:1

##  [1]  0  2  0  4  0  6  0  8  0 10  0 12  0 14  0 16  0 18  0 20

Create a vector with values 1, 0, 3, 0, 5, …, 17, 0, 19, 0.

1:20 * 1:0

##  [1]  1  0  3  0  5  0  7  0  9  0 11  0 13  0 15  0 17  0 19  0

- Create a vector with first 20 powers of 2.

2 ^ (1:20)

##  [1]       2       4       8      16      32      64     128     256     512
## [10]    1024    2048    4096    8192   16384   32768   65536  131072  262144
## [19]  524288 1048576

- Create a vector with values 1, 10, 100, 1000, 10000:

10 ^ (0:4)

## [1]     1    10   100  1000 10000

- Calculate a sum of a sequence \(\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\ldots+\frac{1}{50 \cdot 51}\).

sum(1 / (1:50 * 2:51))

## [1] 0.9803922

- Calculate a sum of a sequence \(\frac{1}{2^{0}}+\frac{1}{2^{1}}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\ldots \frac{1}{2^{20}}\).

sum(1 / 2 ^ (0:20))

## [1] 1.999999

- Calculate a sum of a sequence \(1+\frac{4}{3}+\frac{7}{9}+\frac{10}{27}+\frac{13}{81}+\ldots+\frac{28}{19683}\).

sum((3 * (1:10) - 2) / 3 ^ (0:9))

## [1] 3.749174

- How many numbers from sequence \(1+\frac{4}{3}+\frac{7}{9}+\frac{10}{27}+\frac{13}{81}+\ldots+\frac{28}{19683}\) are bigger than 0.5?

sum((3 * (1:10) - 2) / 3 ^ (0:9) > 0.5)

## [1] 3

20.5 Indexing vectors

Create a vector troiki with values 3, 6, 9, …, 24, 27.

troiki <- seq(3, 27, 3)
troiki

## [1]  3  6  9 12 15 18 21 24 27

Extract the 2nd, 5th and 7th value from the vector troiki.

troiki[c(2, 5, 7)]

## [1]  6 15 21

Extract the last but one value from the vector troiki.

troiki[length(troiki) - 1]

## [1] 24

Exctract all values except the last but one from the vector troiki:

troiki[-(length(troiki) - 1)]

## [1]  3  6  9 12 15 18 21 27

Create a vector vec3:

vec3 <- c(3, 5, 2, 1, 8, 4, 9, 10, 3, 15, 1, 11)

Find the second value of the vector vec3.

vec3[2]

## [1] 5

Find the 2nd and the 5th value from the vector vec3.

vec3[c(2, 5)]

## [1] 5 8

Try to extract the 100th value of the vector vec3:

vec3[100]

## [1] NA

Return all values from the vector vec3 except the second one.

vec3[-2]

##  [1]  3  2  1  8  4  9 10  3 15  1 11

Return all values from the vector vec3 except the second and the fifth values.

vec3[c(-2, -5)]

##  [1]  3  2  1  4  9 10  3 15  1 11

Find the last value of the vector vec3.

vec3[length(vec3)]

## [1] 11

Return all the values of the vector vec3 except the first one and the last one.

vec3[c(-1, -length(vec3))]

##  [1]  5  2  1  8  4  9 10  3 15  1

Find all values of the vector vec3, that are more than 4.

vec3[vec3 > 4]

## [1]  5  8  9 10 15 11

Find all values of the vector vec3, that are more than 4 but less than 10.

Use logical operators if you want to do the task in one line of code!

vec3[vec3 > 4 & vec3 < 10]

## [1] 5 8 9

Find all values of the vector vec3, that are less than 4 or more than 10.

vec3[vec3 < 4 | vec3 > 10]

## [1]  3  2  1  3 15  1 11

Return squares for each value of the vector vec3.

vec3 ^ 2

##  [1]   9  25   4   1  64  16  81 100   9 225   1 121

*Calculate square for each value in odd position and calculate square root for each value in even position of the vector vec3.

Calculating square root is identical to calculating of power of 0.5.

vec3 ^ c(2, 0.5)

##  [1]  9.000000  2.236068  4.000000  1.000000 64.000000  2.000000 81.000000
##  [8]  3.162278  9.000000  3.872983  1.000000  3.316625

Create a vector 2, 4, 6, … , 18, 20 by two other ways.

The more ways to solve a problems you know the better.

(1:20)[c(FALSE,TRUE)]

##  [1]  2  4  6  8 10 12 14 16 18 20

#(1:10)*2

20.6 Missing values

Create a vector vec4 with values 300, 15, 8, 2, 0, 1, 110:

vec4 <- c(300, 15, 8, 20, 0, 1, 110)
vec4

## [1] 300  15   8  20   0   1 110

Replace all values of the vector vec4 that are greater than 20 with NA.

vec4[vec4 > 20] <- NA

Check the vector vec4:

vec4

## [1] NA 15  8 20  0  1 NA

Sum over the vector vec4 using function sum(). The answer NA is not a valid answer!

sum(vec4, na.rm = TRUE)

## [1] 44

20.7 Matrix

Create a 4x4 matrix M1 containing ones.

M1 <- matrix(rep(1, 16), ncol = 4)
M1

##      [,1] [,2] [,3] [,4]
## [1,]    1    1    1    1
## [2,]    1    1    1    1
## [3,]    1    1    1    1
## [4,]    1    1    1    1

Replace all values of M1 that are not on the border (i.e. on positions [2,2], [2,3], [3,2] and [3,3]) with 2.

M1[2:3, 2:3] <- 2
M1

##      [,1] [,2] [,3] [,4]
## [1,]    1    1    1    1
## [2,]    1    2    2    1
## [3,]    1    2    2    1
## [4,]    1    1    1    1

Return the second and the third columns of the matrix M1.

M1[,2:3]

##      [,1] [,2]
## [1,]    1    1
## [2,]    2    2
## [3,]    2    2
## [4,]    1    1

Compare (==) the second column and the second row of the matrix M1.

M1[,2] == M1[2,]

## [1] TRUE TRUE TRUE TRUE

*Create the multiplication table (9х9) as a matrix mult_tab.

mult_tab <- matrix(rep(1:9, rep(9,9))*(1:9), nrow = 9)
mult_tab

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
##  [1,]    1    2    3    4    5    6    7    8    9
##  [2,]    2    4    6    8   10   12   14   16   18
##  [3,]    3    6    9   12   15   18   21   24   27
##  [4,]    4    8   12   16   20   24   28   32   36
##  [5,]    5   10   15   20   25   30   35   40   45
##  [6,]    6   12   18   24   30   36   42   48   54
##  [7,]    7   14   21   28   35   42   49   56   63
##  [8,]    8   16   24   32   40   48   56   64   72
##  [9,]    9   18   27   36   45   54   63   72   81

#Еще
#outer(1:9, 1:9, "*")
#1:9 %o% 1:9

*Select a smaller matrix from the matrix mult_tab that contains only rows from 6 to 8 and columns from 3 to 7.

mult_tab[6:8, 3:7]

##      [,1] [,2] [,3] [,4] [,5]
## [1,]   18   24   30   36   42
## [2,]   21   28   35   42   49
## [3,]   24   32   40   48   56

*Create a logical matrix with TRUE if there is a two-digit number on a corresponding position of the matrix mult_tab and FALSE otherwise.

Matrix is basically a vector. You can work with a matrix the same way you work with a vector — with the only one index.

mult_tab >= 10

##        [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]  [,8]  [,9]
##  [1,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [2,] FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [3,] FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [4,] FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [5,] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [6,] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [7,] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [8,] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [9,] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

*Create a matrix mult_tab2 from the matrix mult_tab where all values that are less than 0 replaced with 10.

mult_tab2 <- mult_tab
mult_tab2[mult_tab < 10] <- 0
mult_tab2

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
##  [1,]    0    0    0    0    0    0    0    0    0
##  [2,]    0    0    0    0   10   12   14   16   18
##  [3,]    0    0    0   12   15   18   21   24   27
##  [4,]    0    0   12   16   20   24   28   32   36
##  [5,]    0   10   15   20   25   30   35   40   45
##  [6,]    0   12   18   24   30   36   42   48   54
##  [7,]    0   14   21   28   35   42   49   56   63
##  [8,]    0   16   24   32   40   48   56   64   72
##  [9,]    0   18   27   36   45   54   63   72   81

20.8 List

Create a list list1:

list1 = list(numbers = 1:5, letters = letters, logic = TRUE)
list1

## $numbers
## [1] 1 2 3 4 5
## 
## $letters
##  [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s"
## [20] "t" "u" "v" "w" "x" "y" "z"
## 
## $logic
## [1] TRUE

Find the first element of the list list1. The answer must be a list with length 1.

list1[1]

## $numbers
## [1] 1 2 3 4 5

Extract the content of the first element of list1 by two different ways. The answer must be a vector.

list1[[1]]

## [1] 1 2 3 4 5

list1$numbers

## [1] 1 2 3 4 5

Find the first value from the first item of the list list1. The answer must be a vector.

list1[[1]][1]

## [1] 1

Create a list list2, that contains two lists list1. One of them must be named pupa, the second one — lupa.

list2 = list(pupa = list1, lupa = list1)
list2

## $pupa
## $pupa$numbers
## [1] 1 2 3 4 5
## 
## $pupa$letters
##  [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s"
## [20] "t" "u" "v" "w" "x" "y" "z"
## 
## $pupa$logic
## [1] TRUE
## 
## 
## $lupa
## $lupa$numbers
## [1] 1 2 3 4 5
## 
## $lupa$letters
##  [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s"
## [20] "t" "u" "v" "w" "x" "y" "z"
## 
## $lupa$logic
## [1] TRUE

*Extract the first item of the list2, then extract the second item from this item, and then extract the third value of it.

list2[[1]][[2]][3]

## [1] "c"

20.9 Датафрейм

Запустите команду data(mtcars) чтобы загрузить встроенный датафрейм с информацией про автомобили. Каждая строчка датафрейма - модель автомобиля, каждая колонка - отдельная характеристика. Подробнее см. ?mtcars.

data(mtcars)
mtcars

Изучите структуру датафрейма mtcars с помощью функции str().

str(mtcars)

## 'data.frame':    32 obs. of  11 variables:
##  $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
##  $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
##  $ disp: num  160 160 108 258 360 ...
##  $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
##  $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
##  $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
##  $ qsec: num  16.5 17 18.6 19.4 17 ...
##  $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
##  $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
##  $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
##  $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

Найдите значение третьей строчки четвертого столбца датафрейма mtcars.

mtcars[3, 4]

## [1] 93

Извлеките первые шесть строчек и первые шесть столбцов датафрейма mtcars.

mtcars[1:6, 1:6]

Извлеките колонку wt датафрейма mtcars - массу автомобиля в тысячах фунтов.

mtcars$wt

##  [1] 2.620 2.875 2.320 3.215 3.440 3.460 3.570 3.190 3.150 3.440 3.440 4.070
## [13] 3.730 3.780 5.250 5.424 5.345 2.200 1.615 1.835 2.465 3.520 3.435 3.840
## [25] 3.845 1.935 2.140 1.513 3.170 2.770 3.570 2.780

Извлеките колонки из mtcars в следующем порядке: hp, mpg, cyl.

mtcars[, c("hp", "mpg", "cyl")]

Посчитайте количество автомобилей с 4 цилиндрами (cyl) в датафрейме mtcars.

sum(mtcars$cyl == 4)

## [1] 11

Посчитайте долю автомобилей с 4 цилиндрами (cyl) в датафрейме mtcars.

mean(mtcars$cyl == 4)

## [1] 0.34375

Найдите все автомобили мощностью не менее 100 лошадиных сил (hp) в датафрейме mtcars.

mtcars[mtcars$hp >= 100, ]

Найдите все автомобили мощностью не менее 100 лошадиных сил (hp) и 4 цилиндрами (cyl) в датафрейме mtcars.

mtcars[mtcars$hp >= 100 & mtcars$cyl == 4, ]

Посчитайте максимальную массу (wt) автомобиля в выборке, воспользовавшись функцией max():

max(mtcars$wt)

## [1] 5.424

Посчитайте минимальную массу (wt) автомобиля в выборке, воспользовавшись функцией min():

min(mtcars$wt)

## [1] 1.513

Найдите строчку датафрейма mtcars с самым легким автомобилем.

mtcars[mtcars$wt == min(mtcars$wt), ]

Извлеките строчки датафрейма mtcars с автомобилями, масса которых ниже средней массы.

mtcars[mtcars$wt < mean(mtcars$wt), ]

Масса автомобиля указана в тысячах фунтов. Создайте колонку wt_kg с массой автомобиля в килограммах. Результат округлите до целых значений с помощью функции round().

1 фунт = 0.45359237 кг.

mtcars$wt_kg <- round(mtcars$wt * 1000 * 0.45359237)
mtcars

20.10 Условные конструкции

Создайте вектор vec5:

vec5 <- c(5, 20, 30, 0, 2, 9)

Создайте новый строковый вектор, где на месте чисел больше 10 в vec5 будет стоять “большое число,” а на месте остальных чисел — “маленькое число.”

ifelse(vec5 > 10, "большое число", "маленькое число")

## [1] "маленькое число" "большое число"   "большое число"   "маленькое число"
## [5] "маленькое число" "маленькое число"

Загрузите файл heroes_information.csv в переменную heroes.

heroes <- read.csv("data/heroes_information.csv", 
                   stringsAsFactors = FALSE,
                   na.strings = c("-", "-99"))

Создайте новою колонку hair в heroes, в которой будет значение "Bold" для тех супергероев, у которых в колонке Hair.color стоит "No Hair", и значение "Hairy" во всех остальных случаях.

heroes$hair <- ifelse(heroes$Hair.color == "No Hair", "Bold", "Hairy")
head(heroes)

Создайте новою колонку tall в heroes, в которой будет значение "tall" для тех супергероев, у которых в колонке Height стоит число больше 190, значение "short" для тех супергероев, у которых в колонке Height стоит число меньше 170, и значение "middle" во всех остальных случаях.

# heroes$tall <- dplyr::case_when(
#   heroes$Height > 190 ~ "tall",
#   heroes$Height < 170 ~ "short",
#   TRUE ~ "middle"
# )
heroes$tall <- ifelse(heroes$Height > 190, 
                      "tall",
                      ifelse(heroes$Height < 170,
                             "short",
                             "middle"))

20.11 Создание функций

Создайте функцию plus_one(), которая принимает число и возвращает это же число + 1.

plus_one <- function(x) x + 1

Проверьте функцию plus_one() на числе 41.

plus_one(41)

## [1] 42

Создайте функцию circle_area(), которая вычисляет площадь круга по радиусу согласно формуле \(\pi r^2\).

circle_area <- function(r) pi * r ^ 2

Посчитайте площадь круга с радиусом 5.

circle_area(5)

## [1] 78.53982

Создайте функцию cels2fahr(), которая будет превращать градусы по Цельсию в градусы по Фаренгейту.

cels2fahr <- function(x) x * 9 / 5 + 32

Проверьте на значениях -100, -40 и 0, что функция cels2fahr() работает корректно.

cels2fahr(c(-100, -40, 0))

## [1] -148  -40   32

Напишите функцию highlight(), которая принимает на входе строковый вектор, а возвращает тот же вектор, но дополненный значением "***" в начале и конце вектора. Лучше всего это рассмотреть на примере:

highlight <- function(x) c("***", x, "***")

highlight(c("Я", "Бэтмен!"))

## [1] "***"     "Я"       "Бэтмен!" "***"

Теперь сделайте функцию highlight более гибкой. Добавьте в нее параметр wrapper =, который по умолчанию равен "***". Значение параметра wrapper = и будет вставлено в начало и конец вектора.

highlight <- function(x, wrapper = "***") c(wrapper, x, wrapper)

Проверьте написанную функцию на векторе c("Я", "Бэтмен!").

highlight(c("Я", "Бэтмен!"))

## [1] "***"     "Я"       "Бэтмен!" "***"

highlight(c("Я", "Бэтмен!"), wrapper = "__")

## [1] "__"      "Я"       "Бэтмен!" "__"

Создайте функцию trim(), которая будет возвращать вектор без первого и последнего значения (вне зависимости от типа данных).

trim <- function(x) x[c(-1, -length(x))]

Проверьте, что функция trim() работает корректно:

trim(1:7)

## [1] 2 3 4 5 6

trim(letters)

##  [1] "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t"
## [20] "u" "v" "w" "x" "y"

Теперь добавьте в функцию trim() параметр n = со значением по умолчанию 1. Этот параметр будет обозначать сколько значений нужно отрезать слева и справа от вектора.

trim <- function(x, n = 1) x[c(-1:-n, (-length(x)+n-1):-length(x))]

Проверьте полученную функцию:

trim(letters)

##  [1] "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t"
## [20] "u" "v" "w" "x" "y"

trim(letters, n = 2)

##  [1] "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u"
## [20] "v" "w" "x"

Сделайте так, чтобы функция trim() работала корректно с n = 0, т.е. функция возвращала бы исходный вектор без изменений.

trim <- function(x, n = 1) {
  if (n == 0) return(x)
  x[c(-1:-n, (-length(x)+n-1):-length(x))]
}

trim(letters, n = 0)

##  [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s"
## [20] "t" "u" "v" "w" "x" "y" "z"

*Теперь добавьте проверку на адекватность входных данных: функция trim() должна выдавать ошибку, если n = меньше нуля или если n = слишком большой и отрезает все значения вектора:

trim <- function(x, n = 1) {
  if (n < 0) stop("n не может быть меньше нуля!")
  l <- length(x)
  if (n > ceiling(l/2) - 1) stop("n слишком большой!")
  if (n == 0) return(x)
  x[c(-1:-n, (-l+n-1):-l)]
}

*Проверьте полученную функцию trim():

trim(1:6, 3)

## Error in trim(1:6, 3): n слишком большой!

trim(1:6, -1)

## Error in trim(1:6, -1): n не может быть меньше нуля!

Создайте функцию na_n(), которая будет возвращать количество NA в векторе.

na_n <- function(x) sum(is.na(x))

Проверьте функцию na_n() на векторе:

na_n(c(NA, 3:5, NA, 2, NA))

## [1] 3

Напишите функцию factors(), которая будет возвращать все делители числа в виде числового вектора.

Здесь может понадобиться оператор для получения остатка от деления: %%.

factors <- function(x) (1:x)[x %% (1:x) == 0]

Проверьте функцию factors() на простых и сложных числах:

factors(3)

## [1] 1 3

factors(161)

## [1]   1   7  23 161

factors(1984)

##  [1]    1    2    4    8   16   31   32   62   64  124  248  496  992 1984

*Напишите функцию is_prime(), которая проверяет, является ли число простым.

Здесь может пригодиться функция any() - она возвращает TRUE, если в векторе есть хотя бы один TRUE.

is_prime <- function(x) !any(x%%(2:(x-1)) == 0)
#is_prime <- function(x) length(factors(x)) == 2 #Используя уже написанную функцию factors()

Проверьте какие года были для нас простыми, а какие нет:

is_prime(2017)

## [1] TRUE

is_prime(2019)

## [1] FALSE

2019/3 #2019 делится на 3 без остатка

## [1] 673

is_prime(2020)

## [1] FALSE

is_prime(2021)

## [1] FALSE

*Создайте функцию monotonic(), которая возвращает TRUE, если значения в векторе не убывают (то есть каждое следующее - больше или равно предыдущему) или не возврастают.

Полезная функция для этого — diff() — возвращает разницу соседних значений.

monotonic <- function(x) all(diff(x)>=0) | all(diff(x)<=0)

monotonic(1:7)

## [1] TRUE

monotonic(c(1:5,5:1))

## [1] FALSE

monotonic(6:-1)

## [1] TRUE

monotonic(c(1:5, rep(5, 10), 5:10))

## [1] TRUE

Бинарные операторы типа + или %in% тоже представляют собой функции. Более того, мы можем создавать свои бинарные операторы! В этом нет особой сложности — нужно все так же создавать функцию (для двух переменных), главное окружать их % и название обрамлять обратными штрихами `. Например, можно сделать свой бинарный оператор %notin%, который будет выдавать TRUE, если значения слева нет в векторе справа:

`%notin%` <- function(x, y) ! (x %in% y)
1:10 %notin% c(1, 4, 5)

##  [1] FALSE  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE

*Создайте бинарный оператор %without%, который будет возвращать все значения вектора слева без значений вектора справа.

`%without%` <- function(x, y) x[!x %in% y]

c("а", "и", "б", "сидели", "на", "трубе") %without% c("а", "б")

## [1] "и"      "сидели" "на"     "трубе"

*Создайте бинарный оператор %between%, который будет возвращать TRUE, если значение в векторе слева накходится в диапазоне значений вектора справа:

`%between%` <- function(x, y) x >= min(y) & x <= max(y)

1:10 %between% c(1, 4, 5)

##  [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE

20.12 Семейство функций apply()

Создайте матрицу M2:

M2 <- matrix(c(20:11, 11:20), nrow = 5)
M2

##      [,1] [,2] [,3] [,4]
## [1,]   20   15   11   16
## [2,]   19   14   12   17
## [3,]   18   13   13   18
## [4,]   17   12   14   19
## [5,]   16   11   15   20

Посчитайте максимальное значение матрицы M2 по каждой строчке.

apply(M2, 1, max)

## [1] 20 19 18 19 20

Посчитайте максимальное значение матрицы M2 по каждому столбцу.

apply(M2, 2, max)

## [1] 20 15 15 20

Посчитайте среднее значение матрицы M2 по каждой строке.

apply(M2, 1, mean)

## [1] 15.5 15.5 15.5 15.5 15.5

Посчитайте среднее значение матрицы M2 по каждому столбцу.

apply(M2, 2, mean)

## [1] 18 13 13 18

Создайте список list3:

list3 <- list(
  a = 1:5,
  b = 0:20,
  c = 4:24,
  d = 6:3,
  e = 6:25
  )

Найдите максимальное значение каждого вектора списка list3.

sapply(list3, max)

##  a  b  c  d  e 
##  5 20 24  6 25

Посчитайте сумму каждого вектора списка list3.

sapply(list3, sum)

##   a   b   c   d   e 
##  15 210 294  18 310

Посчитайте длину каждого вектора списка list3.

sapply(list3, length)

##  a  b  c  d  e 
##  5 21 21  4 20

Напишите функцию max_item(), которая будет принимать на входе список, а возвращать - (первый) самый длинный его элемент.

Для этого вам может понадобиться функция which.max(), которая возвращает индекс максимального значения (первого, если их несколько).

max_item <- function (x) x[[which.max(sapply(x, length))]]

Проверьте функцию max_item() на списке list3.

max_item(list3)

##  [1]  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Теперь мы сделаем сложный список list4:

list4 <- list(1:3, 3:40, list3)

Посчитайте длину каждого вектора в списке, в т.ч. для списка внутри. Результат должен быть списком с такой же структорой, как и изначальный список list4.

Для этого может понадобиться функция rapply(): recursive lapply

rapply(list4, length, how = "list")

## [[1]]
## [1] 3
## 
## [[2]]
## [1] 38
## 
## [[3]]
## [[3]]$a
## [1] 5
## 
## [[3]]$b
## [1] 21
## 
## [[3]]$c
## [1] 21
## 
## [[3]]$d
## [1] 4
## 
## [[3]]$e
## [1] 20

*Загрузите набор данных heroes и посчитайте, сколько NA в каждом из столбцов.

Для этого удобно использовать ранее написанную функцию na_n().

sapply(heroes, na_n)

##          X       name     Gender  Eye.color       Race Hair.color     Height 
##          0          0         29        172        304        172        217 
##  Publisher Skin.color  Alignment     Weight       hair       tall 
##          0        662          7        239        172        217

*Используя ранее написанную функцию is_prime(), напишите функцию prime_numbers(), которая будет возвращать все простые числа до выбранного числа.

is_prime <- function(x) !any(x %% (2:(x - 1)) == 0)
prime_numbers <- function(x) (2:x)[sapply(2:x, is_prime)]

prime_numbers(200)

##  [1]   3   5   7  11  13  17  19  23  29  31  37  41  43  47  53  59  61  67  71
## [20]  73  79  83  89  97 101 103 107 109 113 127 131 137 139 149 151 157 163 167
## [39] 173 179 181 191 193 197 199

20.13 magrittr::`%>%`

Rewrite the following sentences using pipe %>%:

sqrt(sum(1:10))

## [1] 7.416198

1:10 %>%
  sum() %>%
  sqrt()

abs(min(-5:5))

## [1] 5

-5:5 %>%
  min() %>%
  abs()

c("Корень из", 2, "равен", sqrt(2))

## [1] "Корень из"       "2"               "равен"           "1.4142135623731"

2 %>% c("Корень из", ., "равен", sqrt(.))

20.14 Columns selection: `dplyr::select()`

For solving the next tasks you will need datasets heroes and powers that you can import using the following commands:

library(tidyverse)
heroes <- read_csv("https://raw.githubusercontent.com/Pozdniakov/tidy_stats/master/data/heroes_information.csv",
                   na = c("-", "-99"))
powers <- read_csv("https://raw.githubusercontent.com/Pozdniakov/tidy_stats/master/data/super_hero_powers.csv")

Select the first 4 columns from powers.

powers %>%
  select(1:4)

Select all columns from Reflexes to Empathy in the tibble powers:

powers %>%
  select(Reflexes:Empathy)

Select all columns from the tibble powers except the first one (hero_names):

powers %>%
select(!hero_names)

20.15 Rows selection: `dplyr::slice()` and `dplyr::filter()`

Extract rows that contain information about superheroes which have weight more than 500 kg.

heroes %>% 
  filter(Weight > 500)

Extract rows that contain information about female superheroes which have weight more than 500 kg.

heroes %>% 
  filter(Weight > 500 & Gender == "Female")

Extract rows that contain information about human (race is equal to "Human") female superheroes which have weight more than 500 kg. Select the first 5 rows from that.

heroes %>% 
  filter(Race == "Human" & Gender == "Female") %>%
  slice(1:5)

20.16 Rows sorting: `dplyr::arrange()`

Select columns name, Gender, Height for the tibble heroes and sort them by Height in increasing order.

heroes %>%
  select(name, Gender, Height) %>%
  arrange(Height)

Select columns name, Gender, Height for the tibble heroes and sort them by Height in decreasing order.

heroes %>%
  select(name, Gender, Height) %>%
  arrange(desc(Height))

Select columns name, Gender, Height for the tibble heroes and sort them first by Gender, then by Height in decreasing order.

heroes %>%
  select(name, Gender, Height) %>%
  arrange(Gender, desc(Height))

20.17 Unique values: `dplyr::distinct()`

Exctract unique values from column Eye color in heroes.

heroes %>%
  distinct(`Eye color`)

Exctract unique values from column Hair color in heroes.

heroes %>%
  distinct(`Hair color`)

20.18 Making new columns: `dplyr::mutate()` and `dplyr::transmute()`

Create new column height_m with height of superheroes in meters, then select name and height_m columns.

heroes %>%
  mutate(height_m = Height/100) %>%
  select(name, height_m)

20.19 Агрегация: `dplyr::group_by() %>% summarise()`

Calculate number of superheroes by races and sort it in decreasing order. Extract the first 5 rows.

heroes %>%
  count(Race, sort = TRUE) %>%
  slice(1:5)

Calculate the average height by gender.

heroes %>%
  group_by(Gender) %>%
  summarise(height_mean = mean(Height, na.rm = TRUE))

20.20 Operations with several columns: `across()`

Count number of NA in each column, grouping by Gender.

na_n <- function(x) sum(is.na(x))
heroes %>%
  group_by(Gender) %>%
  summarise(across(everything(), na_n))

Count number of NA in each column that ends with "color", grouping by Gender.

na_n <- function(x) sum(is.na(x))
heroes %>%
  group_by(Gender) %>%
  summarise(across(ends_with("color"), na_n))

20.21 Merging dataframes: *_join {#solution_join}

Create a tibble web creators such that it contains only superheroes that can create web, i.e. they have TRUE in column Web Creation in tibble powers.

powers_web <- powers %>%
  select(hero_names, `Web Creation`)
web_creators <- left_join(heroes, powers_web, by = c("name" = "hero_names")) %>%
  filter(`Web Creation`)
web_creators

Find all superheroes that can be found in heroes but are absent in powers. The answer must be a character vector with superheroes names.

anti_join(heroes, powers, by = c("name" = "hero_names")) %>%
  pull(name)

##  [1] "Agent 13"          "Alfred Pennyworth" "Arsenal"          
##  [4] "Batgirl III"       "Batgirl V"         "Beetle"           
##  [7] "Black Goliath"     "Black Widow II"    "Blaquesmith"      
## [10] "Bolt"              "Boomer"            "Box"              
## [13] "Box III"           "Captain Mar-vell"  "Cat II"           
## [16] "Cecilia Reyes"     "Clea"              "Clock King"       
## [19] "Colin Wagner"      "Colossal Boy"      "Corsair"          
## [22] "Cypher"            "Danny Cooper"      "Darkside"         
## [25] "ERG-1"             "Fixer"             "Franklin Storm"   
## [28] "Giant-Man"         "Giant-Man II"      "Goliath"          
## [31] "Goliath"           "Goliath"           "Guardian"         
## [34] "Hawkwoman"         "Hawkwoman II"      "Hawkwoman III"    
## [37] "Howard the Duck"   "Jack Bauer"        "Jesse Quick"      
## [40] "Jessica Sanders"   "Jigsaw"            "Jyn Erso"         
## [43] "Kid Flash II"      "Kingpin"           "Meteorite"        
## [46] "Mister Zsasz"      "Mogo"              "Moloch"           
## [49] "Morph"             "Nite Owl II"       "Omega Red"        
## [52] "Paul Blart"        "Penance"           "Penance I"        
## [55] "Plastic Lad"       "Power Man"         "Renata Soliz"     
## [58] "Ronin"             "Shrinking Violet"  "Snake-Eyes"       
## [61] "Spider-Carnage"    "Spider-Woman II"   "Stacy X"          
## [64] "Thunderbird II"    "Two-Face"          "Vagabond"         
## [67] "Vision II"         "Vulcan"            "Warbird"          
## [70] "White Queen"       "Wiz Kid"           "Wondra"           
## [73] "Wyatt Wingfoot"    "Yellow Claw"

Find all superheroes that can be found in powers but are absent in heroes. The answer must be a character vector with superheroes names.

anti_join(powers, heroes, by = c("hero_names" = "name")) %>%
  pull(hero_names)

##  [1] "3-D Man"           "Bananaman"         "Bizarro-Girl"     
##  [4] "Black Vulcan"      "Blue Streak"       "Bradley"          
##  [7] "Clayface"          "Concrete"          "Dementor"         
## [10] "Doctor Poison"     "Fire"              "Hellgramite"      
## [13] "Lara Croft"        "Little Epic"       "Lord Voldemort"   
## [16] "Orion"             "Peek-a-Boo"        "Queen Hippolyta"  
## [19] "Reactron"          "SHDB"              "Stretch Armstrong"
## [22] "TEST"              "Tommy Clarke"      "Tyrant"

20.22 Tidy data

First, create a tibble heroes_weight by copying the following code:

heroes_weight <- heroes %>%
  filter(Publisher %in% c("DC Comics", "Marvel Comics")) %>%
  group_by(Gender, Publisher) %>%
  summarise(weight_mean = mean(Weight, na.rm = TRUE)) %>%
  drop_na()
heroes_weight

Turn the tibble heroes_weight into wide tibble.

heroes_weight %>%
  pivot_wider(names_from = "Publisher", values_from = "weight_mean")

Then, convert it back to the long format:

heroes_weight %>%
  pivot_wider(names_from = "Publisher", values_from = "weight_mean") %>%
  pivot_longer(cols = !Gender,
               names_to = "Publisher",
               values_to = "weight_mean")

Turn the tibble powers into a long tibble with three columns: hero_names, power (superpower names) and has (does this superhero have this ability?).

powers %>%
  pivot_longer(cols = !hero_names,
               names_to = "power",
               values_to = "has")

Turn the tibble powers into wide form again but with the new structure: each row is a superpower, each column is a superhero (except for the first column - superpower name).

powers %>%
  pivot_longer(cols = !hero_names,
               names_to = "power",
               values_to = "has") %>%
  pivot_wider(names_from = hero_names,
              values_from = has)

20.23 Описательная статистика

Для выполнения задания создайте вектор height из колонки Height датасета heroes, удалив в нем NA.

height <- heroes %>%
  drop_na(Height) %>%
  pull(Height)

Посчитайте среднее в векторе height.

mean(height)

## [1] 186.7263

Посчитайте усеченное среднее в векторе height с усечением 5% значений с обоих сторон.

mean(height, trim = 0.05)

## [1] 182.5846

Посчитайте медиану в векторе height.

median(height)

## [1] 183

Посчитайте стандартное отклонение в векторе height.

sd(height)

## [1] 59.25189

Посчитайте межквартильный размах в векторе height.

IQR(height)

## [1] 18

Посчитайте ассиметрию в векторе height.

psych::skew(height)

## [1] 8.843432

Посчитайте эксцесс в векторе height.

psych::kurtosi(height)

## [1] 105.0297

Примените функции для получения множественных статистик на векторе height.

summary(height)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    15.2   173.0   183.0   186.7   191.0   975.0

psych::describe(height)

skimr::skim(height)

Таблица 20.1: Data summary
Name	height
Number of rows	517
Number of columns	1
_______________________
Column type frequency:
numeric	1
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
data	0	1	186.73	59.25	15.2	173	183	191	975	▇▁▁▁▁

20.24 Построение графиков в `ggplot2`

Нарисуйте столбиковую диаграмму (geom_bar()), которая будет отражать количество супергероев издателей "Marvel Comics", "DC Comics" и всех остальных (отдельным столбиком) из датасета heroes.

heroes %>%
  mutate(Publisher = ifelse(Publisher %in% c("Marvel Comics", "DC Comics"), 
                            Publisher,
                            "Other publishers")) %>%
  #mutate(Publisher = fct_lump(Publisher, 2)) %>% #Еще один способ сделать то же самое, но через forcats
  ggplot(aes(x = Publisher)) +
  geom_bar()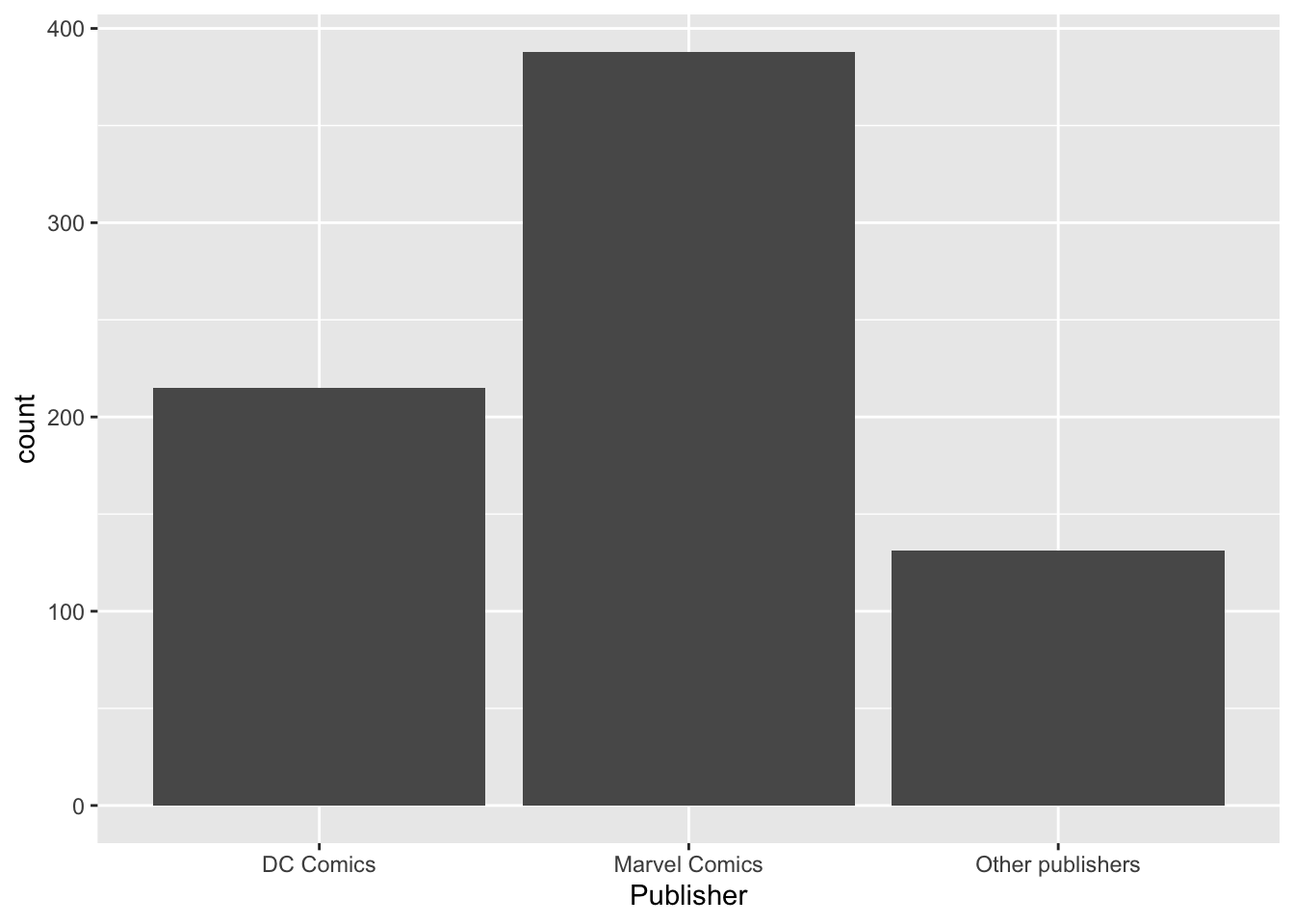

Добавьте к этой диаграме заливку цветом (fill =) в зависимости от распределения Gender внутри каждой группы.

heroes %>%
  mutate(Publisher = ifelse(Publisher %in% c("Marvel Comics", "DC Comics"), 
                            Publisher,
                            "Other publishers")) %>%
  #mutate(Publisher = fct_lump(Publisher, 2)) %>% #Еще один способ сделать то же самое, но через forcats
  ggplot(aes(x = Publisher, fill = Gender)) +
  geom_bar()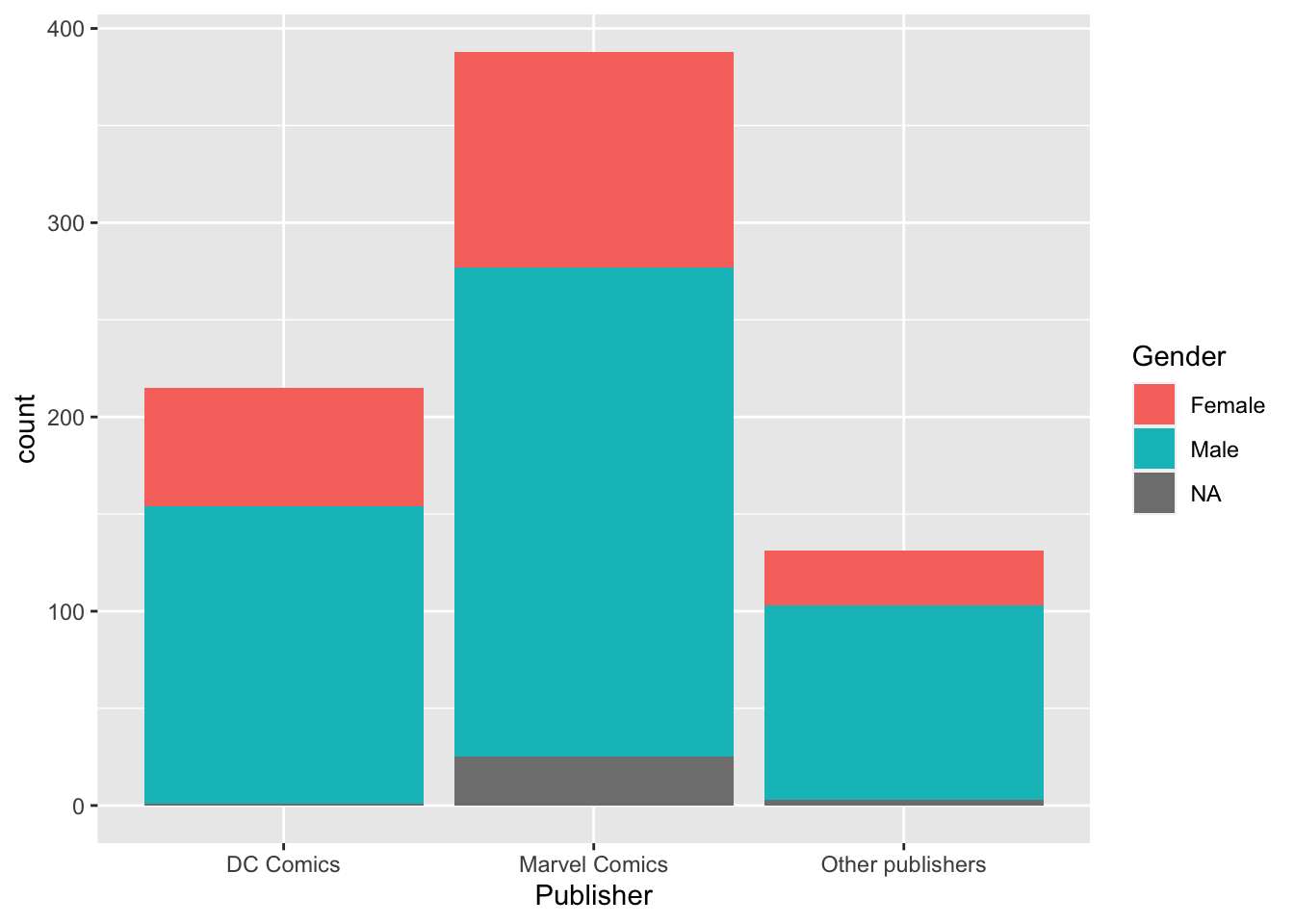

Сделайте так, чтобы каждый столбик был максимальной высоты (position = "fill").

heroes %>%
  mutate(Publisher = ifelse(Publisher %in% c("Marvel Comics", "DC Comics"), 
                            Publisher,
                            "Other publishers")) %>%
  #mutate(Publisher = fct_lump(Publisher, 2)) %>% #Еще один способ сделать то же самое, но через forcats
  ggplot(aes(x = Publisher, fill = Gender)) +
  geom_bar(position = "fill")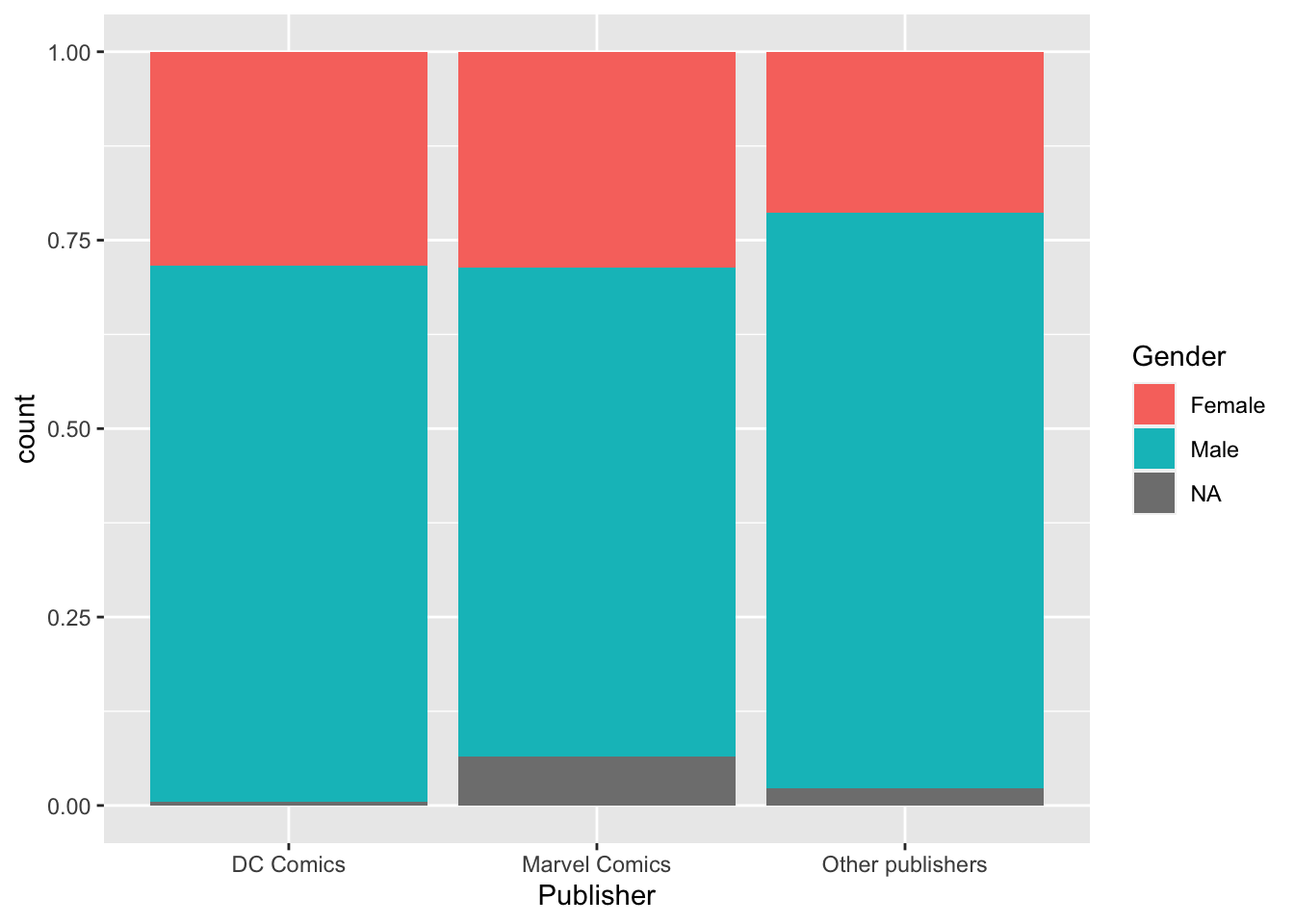

Финализируйте график, задав ему описания осей (например, функция labs()), использовав процентную шкалу (scale_y_continuous(labels = scales::percent)) и задав тему theme_minimal().

heroes %>%
  mutate(Publisher = ifelse(Publisher %in% c("Marvel Comics", "DC Comics"), 
                            Publisher,
                            "Other publishers")) %>%
  #mutate(Publisher = fct_lump(Publisher, 2)) %>% #Еще один способ сделать то же самое, но через forcats
  ggplot(aes(x = Publisher, fill = Gender)) +
  geom_bar(position = "fill") +
  labs(title = "Распределение супергероев по полу у разных издателей коммиксов",
       x = "Издатель",
       y = "Количество супергероев")+
  scale_y_continuous(labels = scales::percent) +
  theme_minimal()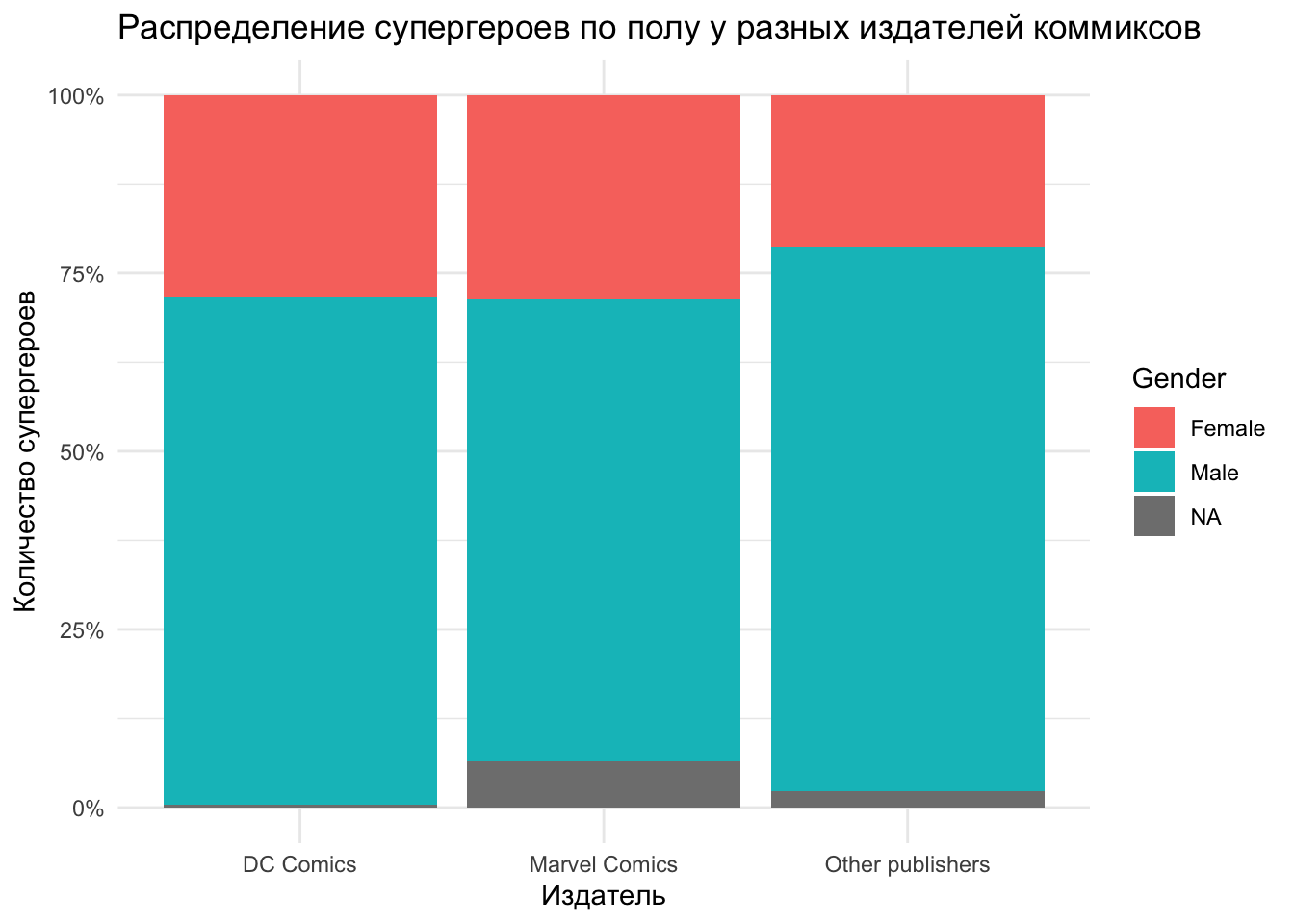

Создайте диаграмму рассеяния для датасета heroes, для которой координаты по оси x будут взяты из колонки Height, а координаты по оси y — из колонки Weight.

heroes %>%
  ggplot(aes(x = Height, y = Weight)) +
  geom_point()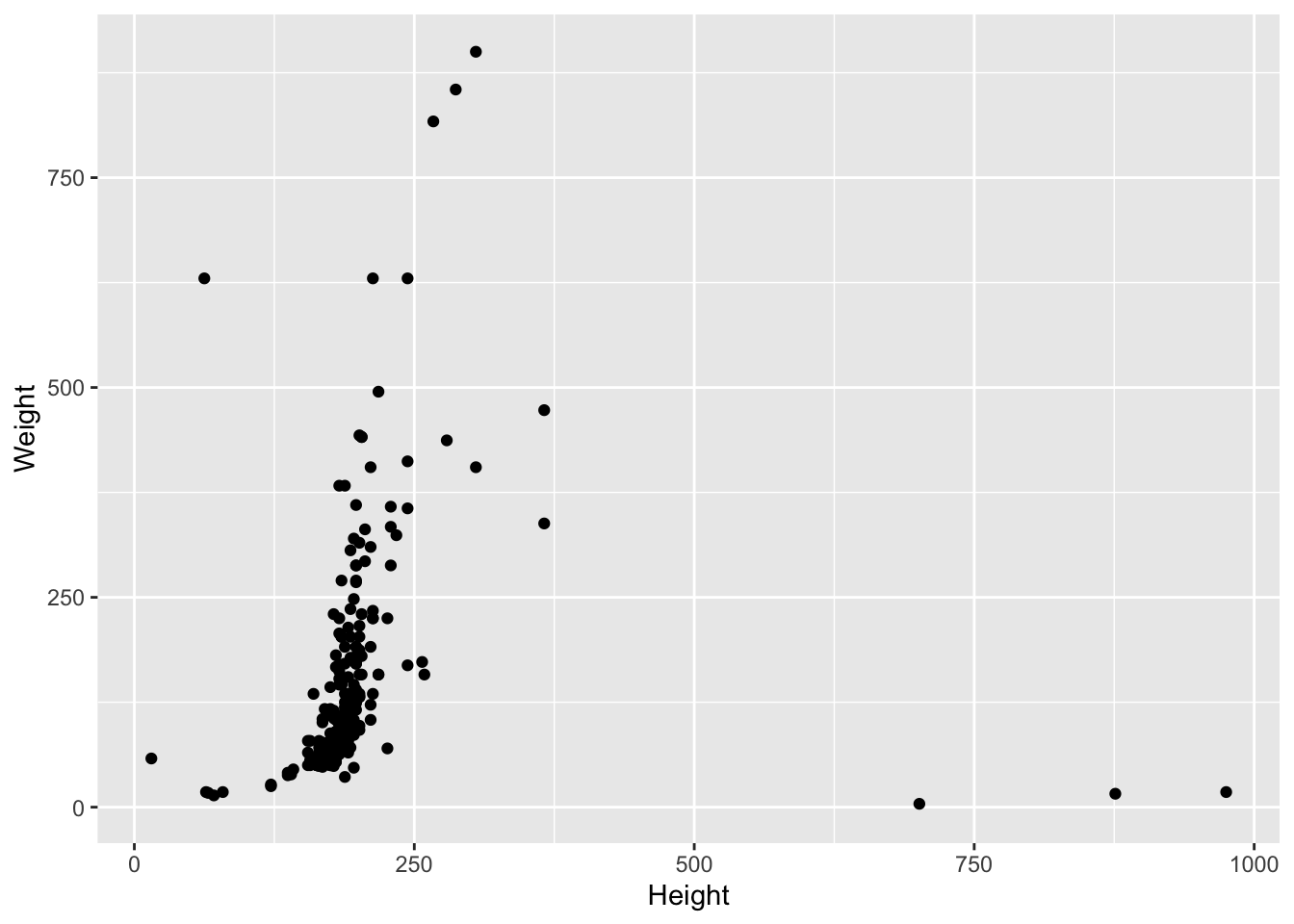

Удалите с графика все экстремальные значения, для которых Weight больше или равен 700 или Height больше или равен 400. (Подсказка: это можно делать как средствами ggplot2, так и функцией filter() из dplyr).

heroes %>%
  filter(Weight < 700 & Height < 400) %>%
  ggplot(aes(x = Height, y = Weight)) +
  geom_point()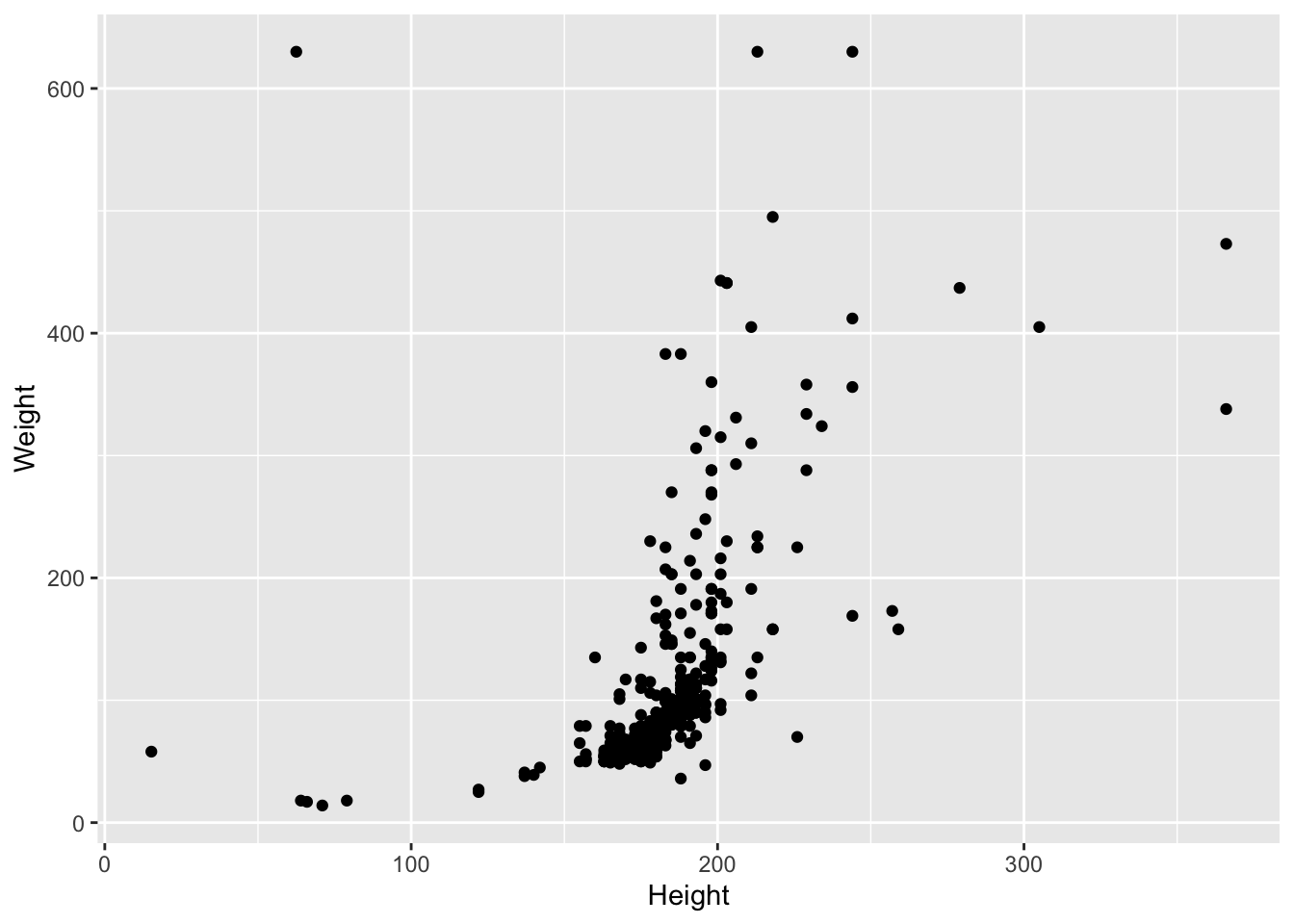

Раскрасьте точки в зависимости от Gender, сделайте их полупрозрачными ( параметр alpha =).

heroes %>%
  filter(Weight < 700 & Height < 400) %>%
  ggplot(aes(x = Height, y = Weight)) +
  geom_point(aes(colour = Gender), alpha = 0.5)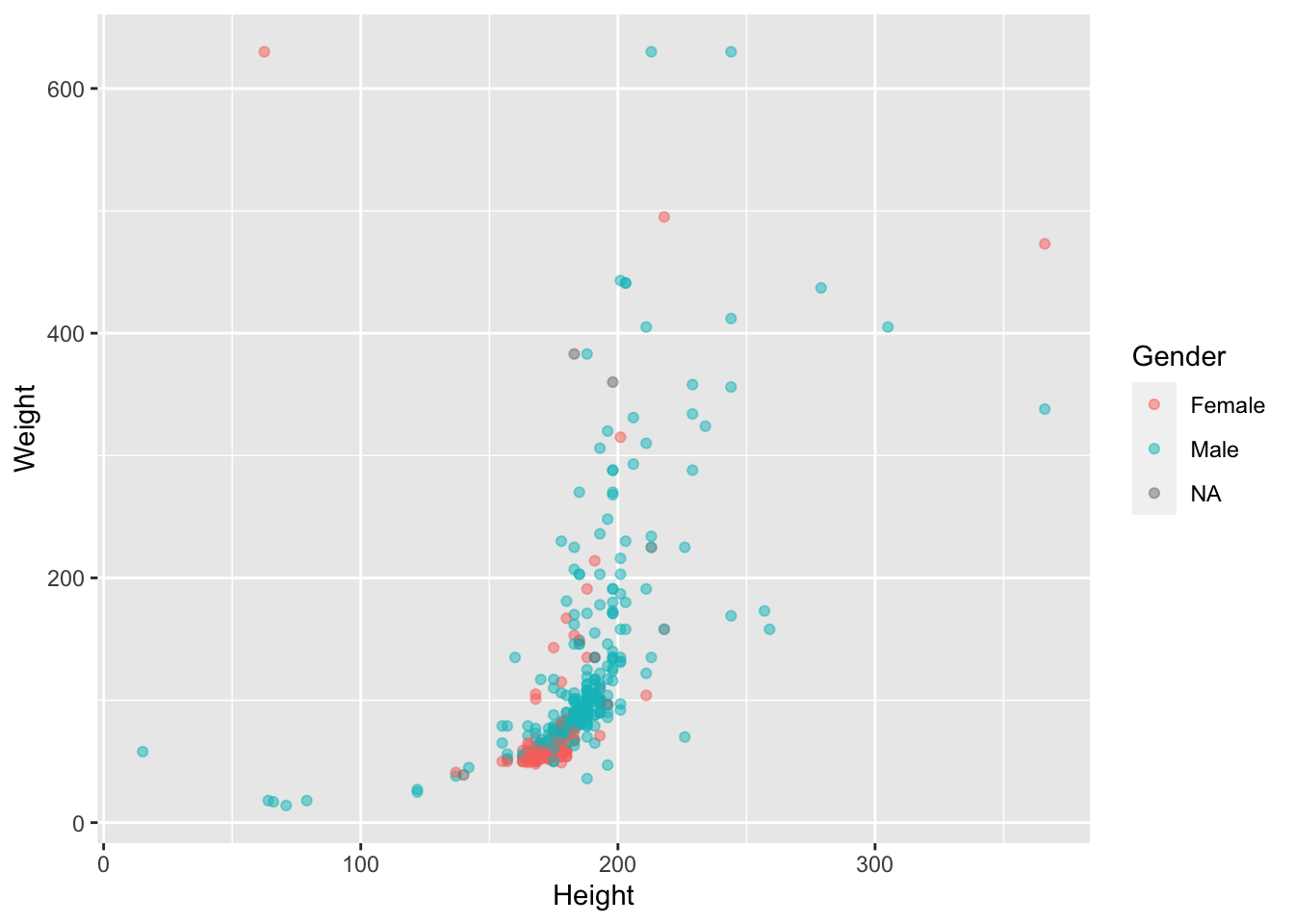

Сделайте так, чтобы координатная плоскость имела соотношение 1:1 шкал по оси x и y. Этого можно добиться с помощью функции coord_fixed().

heroes %>%
  filter(Weight < 700 & Height < 400) %>%
  ggplot(aes(x = Height, y = Weight)) +
  geom_point(aes(colour = Gender), alpha = 0.5) +
  coord_fixed()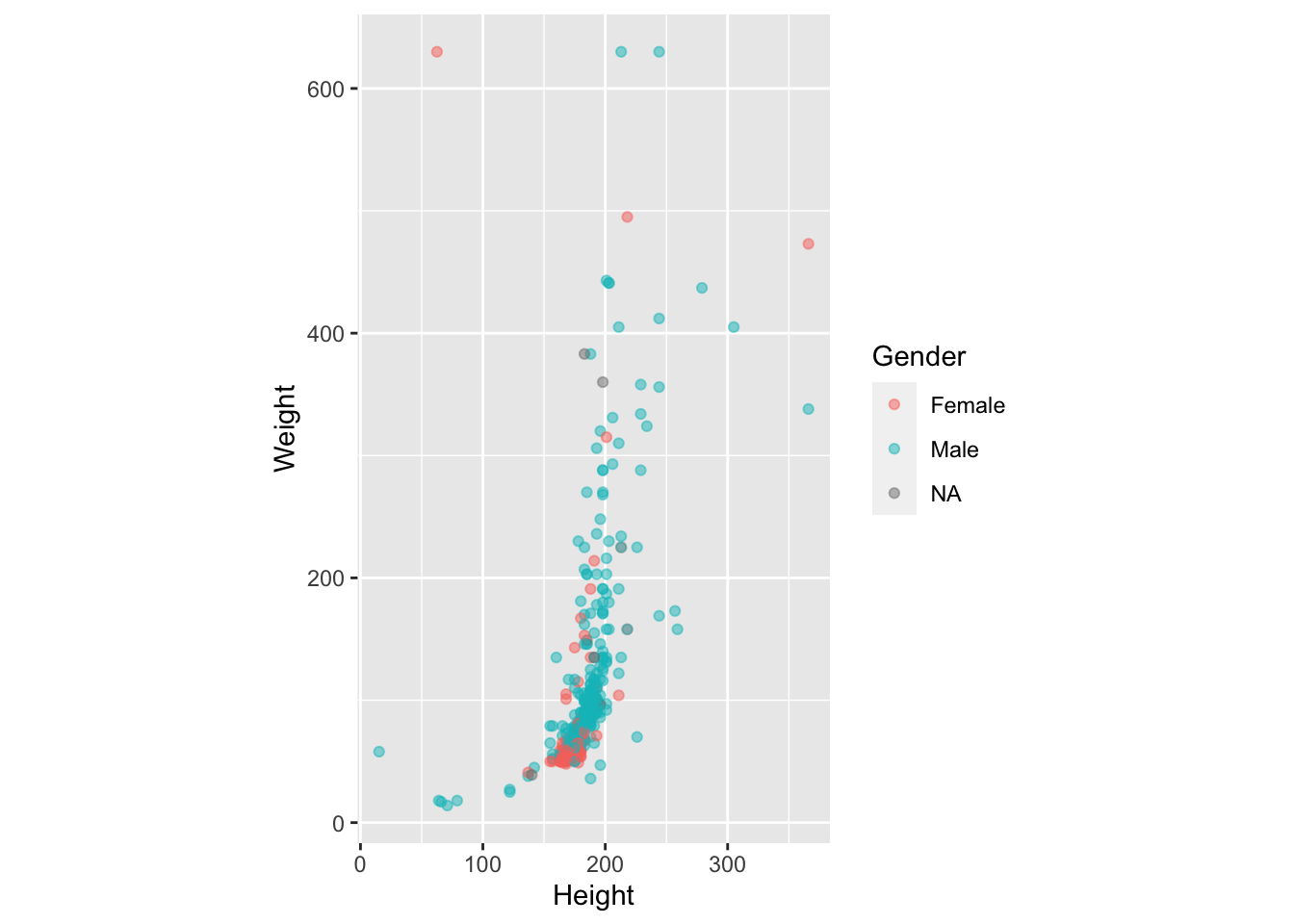

Разделите график (facet_wrap()) на три: для "DC Comics","Marvel Comics" и всех остальных.

heroes %>%
  mutate(Publisher = ifelse(Publisher %in% c("Marvel Comics", "DC Comics"), 
                            Publisher,
                            "Other publishers")) %>%
  filter(Weight < 700 & Height < 400) %>%
  ggplot(aes(x = Height, y = Weight)) +
  geom_point(aes(colour = Gender), alpha = 0.5) +
  coord_fixed() +
  facet_wrap(~Publisher)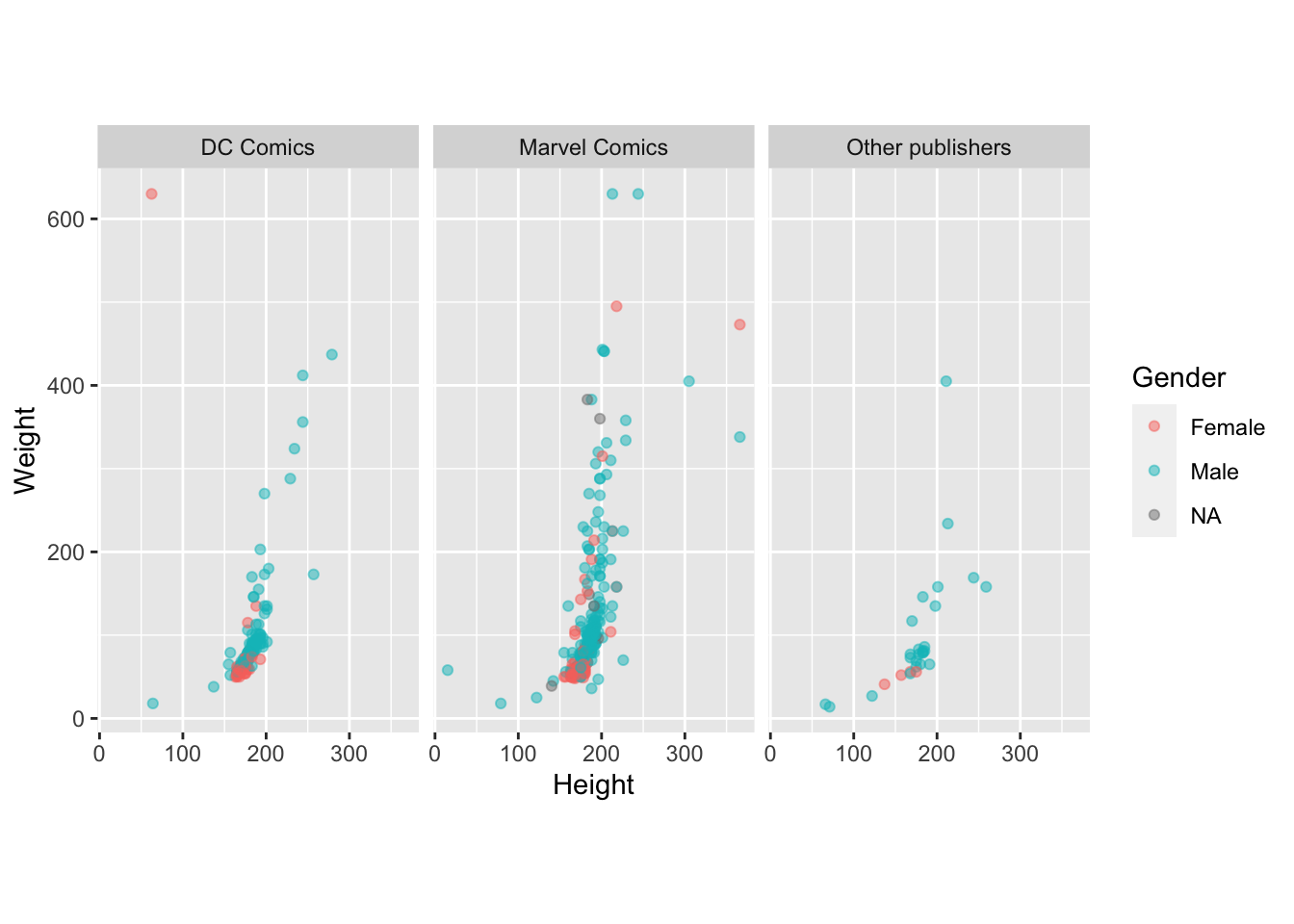

Используйте для графика тему theme_linedraw().

heroes %>%
  mutate(Publisher = ifelse(Publisher %in% c("Marvel Comics", "DC Comics"), 
                            Publisher,
                            "Other publishers")) %>%
  filter(Weight < 700 & Height < 400) %>%
  ggplot(aes(x = Height, y = Weight)) +
  geom_point(aes(colour = Gender), alpha = 0.5) +
  coord_fixed() +
  facet_wrap(~Publisher)+
  theme_linedraw()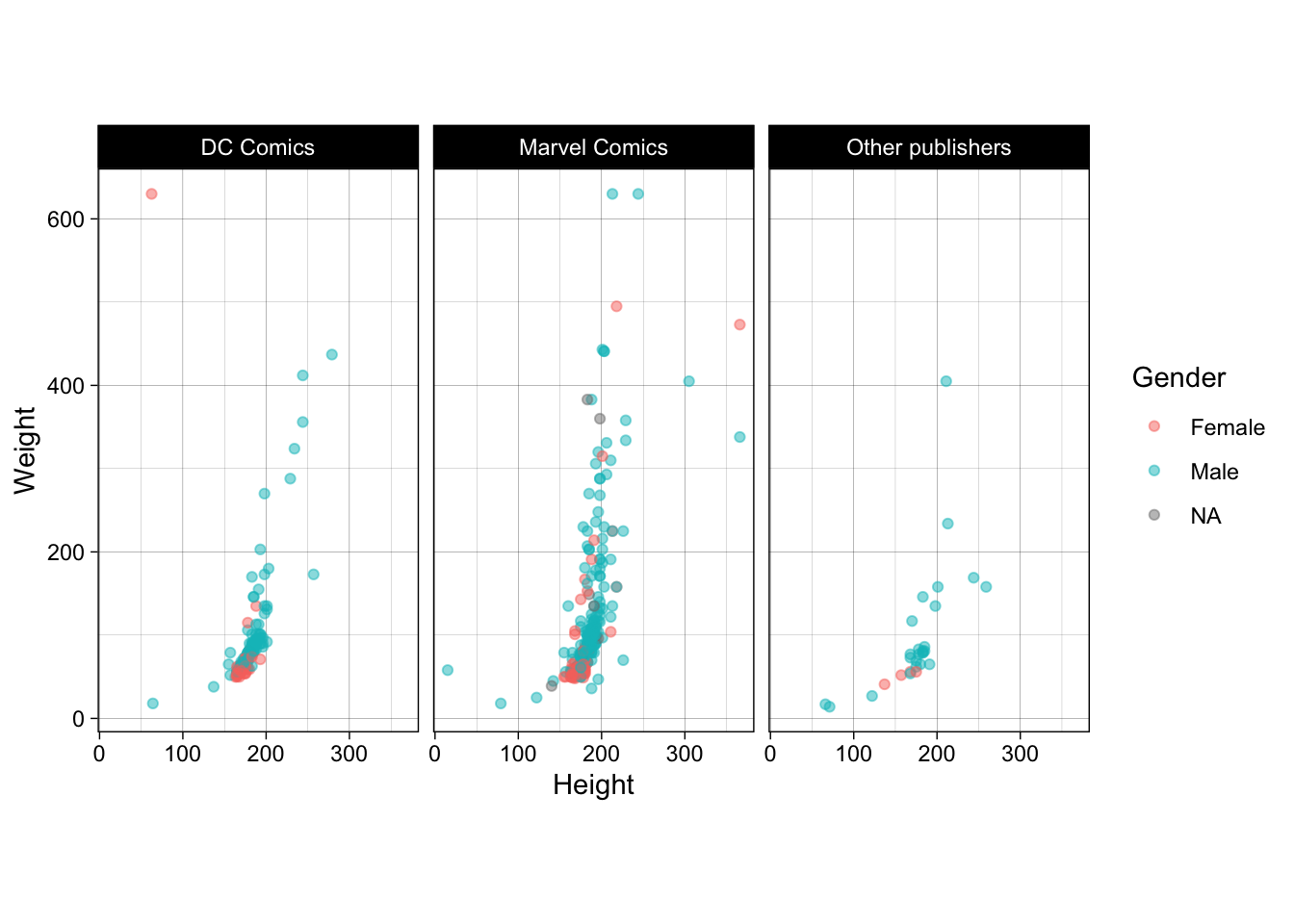

- Постройте новый график (или возьмите старый) по датасетам heroes и/или powers и сделайте его некрасивым! Чем хуже у вас получится график, тем лучше. Желательно, чтобы этот график был по-прежнему графиком, а не произведением абстрактного искусства. Разница очень тонкая, но она есть.

Вот несколько подсказок для этого задания:

Для вдохновения посмотрите на вот эти графики.
Для реально плохих графиков вам придется покопаться с настройками темы. Посмотрите подсказку по темам ?theme, попытайтесь что-то поменять в теме.
Экспериментируйте с разными геомами и необычными их применениями.
По изучайте дополнения к gpplot2.
Попробуйте подготовить интересные данные для этого графика.

НЕТ ПРАВИЛЬНОГО РЕШЕНИЯ, ПРОЯВИТЕ СВОЮ ФАНТАЗИЮ!

20.25 Распределения

Выберите любое непрерывное распределение из представленных в базовом пакете stats или же в любом другом пакете. Найти все распределения пакета stats можно с помощью ?Distributions. Подберите для него какие-нибудь параметры или используйте параметры по умолчанию.

Я возьму F-распределение с параметрами df1 = 4 и df = 10, но вы можете выбрать другое распределение.

Визуализируйте функцию плотности вероятности для выбранного распределения.

v <- seq(0, 5, 0.01)
plot(v, df(v, df1 = 4, df2 = 10))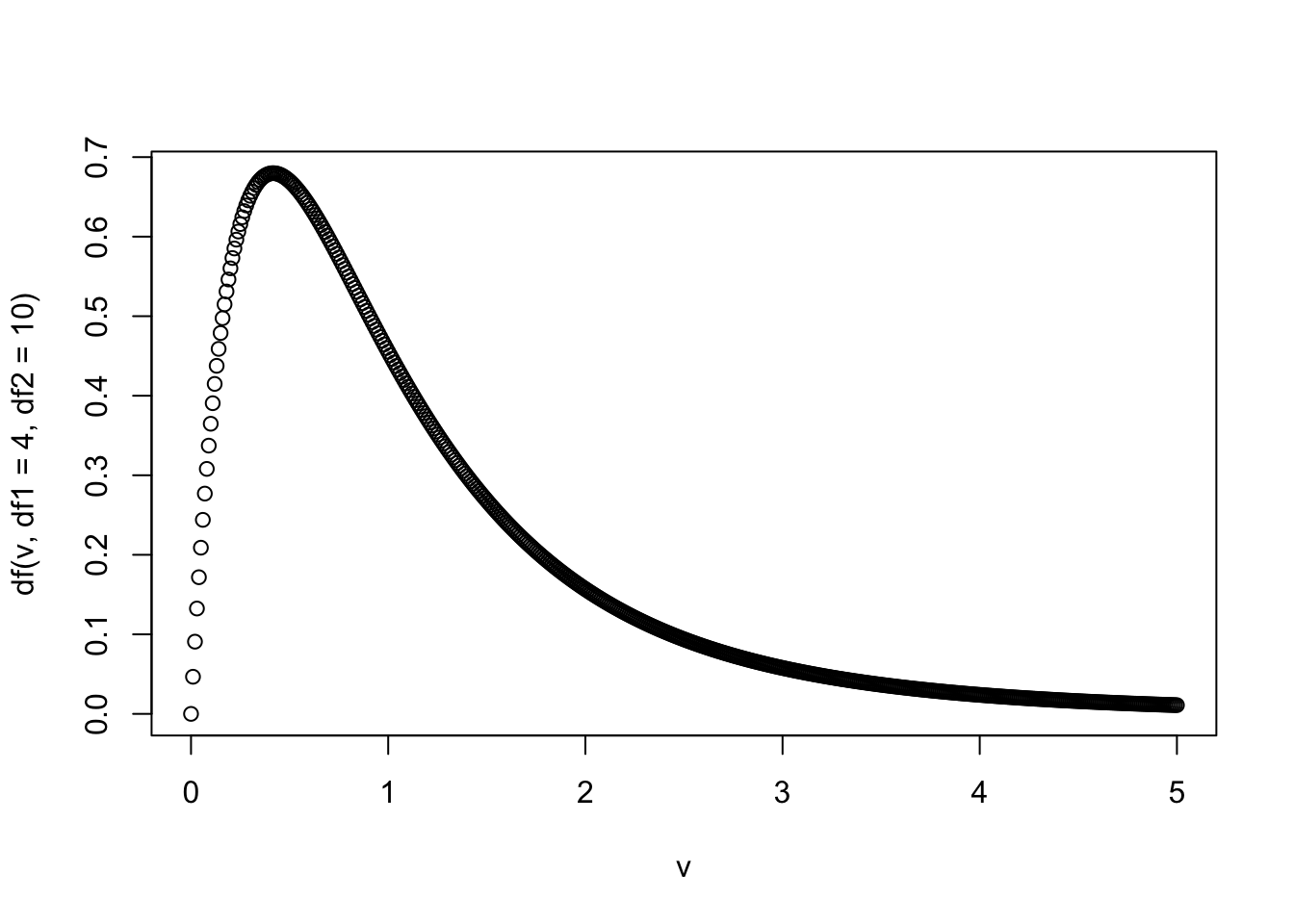

Визуализируйте функцию накопленной плотности распределения для выбранной функции.

plot(v, pf(v, df1 = 4, df2 = 10))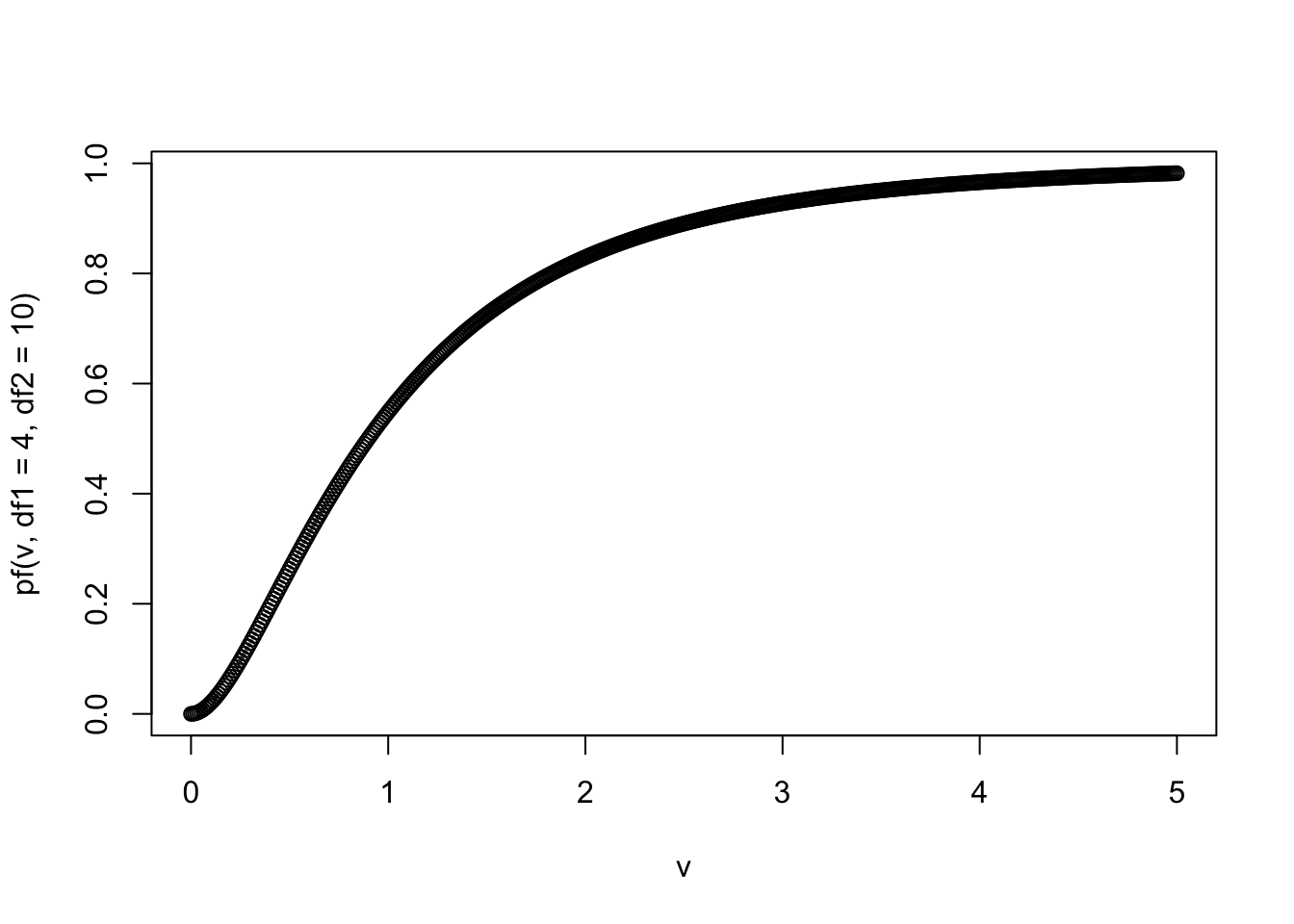

Визуализируйте квантильную функцию для выбранного распределения.

p <- seq(0, 1, .01)
plot(p, qf(p, df1 = 4, df2 = 10))

Сделайте выборку из 100 случайных значений из выбранного распределения и постройте гистограмму (функция hist()) для полученной выборки.

hist(rf(100, df1 = 4, df2 = 10))

20.26 Одновыборочный t-test

Представьте, что наши супергерои из набора данных heroes — это выборка из генеральной совокупности всех написанных и ненаписанных супергероев. Проведите одновыборочный t-тест для веса супергероев и числа 100 — предположительного среднего веса в генеральной совокупности всех супергероев. Проинтерпретируйте результат.

t.test(heroes$Weight, mu = 100)

## 
##  One Sample t-test
## 
## data:  heroes$Weight
## t = 2.6174, df = 494, p-value = 0.009133
## alternative hypothesis: true mean is not equal to 100
## 95 percent confidence interval:
##  103.0549 121.4501
## sample estimates:
## mean of x 
##  112.2525

p-value меньше .05, поэтому мы можем отклонить нулевую гипотезу о том, что среднее для веса в генеральной совкупности, из которой вы взяли выборку супергероев, равно 100. Мы принимаем ненулевую гипотезу о том, что в генеральной совокупности средний вес не равен 100.

Проведите одновыборочный t-тест для роста супергероев и числа 185 — предположительного среднего роста в генеральной совокупности всех супергероев. Проинтерпретируйте результат.

t.test(heroes$Height, mu = 185)

## 
##  One Sample t-test
## 
## data:  heroes$Height
## t = 0.66246, df = 516, p-value = 0.508
## alternative hypothesis: true mean is not equal to 185
## 95 percent confidence interval:
##  181.6068 191.8458
## sample estimates:
## mean of x 
##  186.7263

p-value больше .05, поэтому мы не можем отклонить нулевую гипотезу о том, что среднее для роста в генеральной совкупности, из которой вы взяли выборку супергероев, равно 185.

20.27 Двухвыборочный зависимый t-test

diet <- readr::read_csv("https://raw.githubusercontent.com/Pozdniakov/tidy_stats/master/data/stcp-Rdataset-Diet.csv")

Посчитайте двухвыборочный зависимый т-тест для остальных диет: для диеты 2 и диеты 3. Проинтерпретируйте полученные результаты.

diet2 <- diet %>%
  filter(Diet == 2)
t.test(diet2$pre.weight, diet2$weight6weeks, paired = TRUE)

## 
##  Paired t-test
## 
## data:  diet2$pre.weight and diet2$weight6weeks
## t = 6.231, df = 26, p-value = 1.36e-06
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  2.027715 4.024137
## sample estimates:
## mean of the differences 
##                3.025926

p-value меньше .05, поэтому мы можем отклонить нулевую гипотезу о том, что масса до и после диеты одинаковая. Мы принимаем альтернативную гипотезу о различии средних в генеральной совокупности.

diet3 <- diet %>%
  filter(Diet == 3)
t.test(diet3$pre.weight, diet3$weight6weeks, paired = TRUE)

## 
##  Paired t-test
## 
## data:  diet3$pre.weight and diet3$weight6weeks
## t = 11.167, df = 26, p-value = 2.03e-11
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  4.200493 6.095803
## sample estimates:
## mean of the differences 
##                5.148148

20.28 Двухвыборочный независимый t-test

Сделайте независимый t-тест для сравнения веса испытуемых двух групп после диеты, сравнив вторую и третью группу. Проинтерпретируйте результаты.

diet23 <- diet %>%
  filter(Diet %in% 2:3)
t.test(weight6weeks ~ Diet, data = diet23, paired = FALSE)

## 
##  Welch Two Sample t-test
## 
## data:  weight6weeks by Diet
## t = -0.15686, df = 49.774, p-value = 0.876
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -5.471327  4.678734
## sample estimates:
## mean in group 2 mean in group 3 
##        68.08519        68.48148

p-value больше .05, поэтому мы не можем отклонить нулевую гипотезу о том, что масса до и после диеты одинаковая.

Сделайте независимый t-тест для сравнения веса испытуемых двух групп после диеты, сравнив первую и третью группу. Проинтерпретируйте результаты.

diet13 <- diet %>%
  filter(Diet %in% c(1,3))
t.test(weight6weeks ~ Diet, data = diet13, paired = FALSE)

## 
##  Welch Two Sample t-test
## 
## data:  weight6weeks by Diet
## t = 0.46818, df = 48.072, p-value = 0.6418
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -3.602450  5.789487
## sample estimates:
## mean in group 1 mean in group 3 
##        69.57500        68.48148

p-value больше .05, поэтому мы не можем отклонить нулевую гипотезу о том, что масса до и после диеты одинаковая.

20.29 Непараметрические аналоги t-теста

Сравните вес первой и второй группы после диеты, используя тест Манна-Уитни. Сравните результаты теста Манна-Уитни с результатами t-теста? Проинтерпретируйте полученные результаты.

diet12 <- diet %>%
  filter(Diet %in% c(1,2))
wilcox.test(weight6weeks ~ Diet, data = diet12, paired = FALSE)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  weight6weeks by Diet
## W = 368, p-value = 0.4117
## alternative hypothesis: true location shift is not equal to 0

В обоих случаях p-value больше 0.05, мы не можем отклонить нулевую гипотезу об отсутствии различий.

Повторите задание для второй и третьей группы, а так же для первой и третьей группы.

wilcox.test(weight6weeks ~ Diet, data = diet23, paired = FALSE)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  weight6weeks by Diet
## W = 340.5, p-value = 0.6843
## alternative hypothesis: true location shift is not equal to 0

wilcox.test(weight6weeks ~ Diet, data = diet13, paired = FALSE)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  weight6weeks by Diet
## W = 346, p-value = 0.6849
## alternative hypothesis: true location shift is not equal to 0

В обоих случаях p-value больше 0.05, как и для соответствующих t-тестов. Мы не можем отклонить нулевую гипотезу об отстутствии различий между второй и третьей диетой, между первой и третьей диетой.

Сравните вес до и после для диеты 1, используя тест Уилкоксона. Сравните с результатами применения t-теста. Проинтерпретируйте полученные результаты.

diet1 <- diet %>%
  filter(Diet == 1)
wilcox.test(diet1$pre.weight, diet1$weight6weeks, paired = TRUE)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  diet1$pre.weight and diet1$weight6weeks
## V = 299, p-value = 2.203e-05
## alternative hypothesis: true location shift is not equal to 0

И t-тест, и тест Уилкоксона дают p-value ниже 0.05. Мы можем отклонить нулевую гипотезу об отсутствии различий.

Сравните вес до и после для диеты 2 и диеты 3, используя тест Уилкоксона. Сравните с результатами применения t-теста. Проинтерпретируйте полученные результаты.

wilcox.test(diet2$pre.weight, diet2$weight6weeks, paired = TRUE)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  diet2$pre.weight and diet2$weight6weeks
## V = 313, p-value = 5.419e-05
## alternative hypothesis: true location shift is not equal to 0

wilcox.test(diet3$pre.weight, diet3$weight6weeks, paired = TRUE)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  diet3$pre.weight and diet3$weight6weeks
## V = 378, p-value = 5.912e-06
## alternative hypothesis: true location shift is not equal to 0

В обоих случаях и t-тест, и тест Уилкоксона дают p-value ниже 0.05. Мы можем отклонить нулевую гипотезу об отсутствии различий.

20.30 Исследование набора данных Backpack

Для следующих тем нам понадобится набор данных Backpack из пакета Stat2Data.

#install.packages("Stat2Data")
library(Stat2Data)
data(Backpack)
back <- Backpack %>%
  mutate(backpack_kg = 0.45359237 * BackpackWeight,
         body_kg = 0.45359237 * BodyWeight)

Как различается вес рюкзака в зависимости от пола? Кто весит больше?

back %>%
  group_by(Sex) %>%
  summarise(mean(backpack_kg))

Если допустить, что выборка репрезентативна, то можно ли сделать вывод о различии по среднему весу рюкзаков в генеральной совокупности?

t.test(backpack_kg ~ Sex, data = back)

## 
##  Welch Two Sample t-test
## 
## data:  backpack_kg by Sex
## t = -1.1782, df = 86.25, p-value = 0.242
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.6892365  0.4320067
## sample estimates:
## mean in group Female   mean in group Male 
##             5.006010             5.634625

p-value больше .05, поэтому мы не можем отклонить нулевую гипотезу о том, что масса до и после диеты одинаковая.

Повторите пунктs 2 и 3 для веса самих студентов.

back %>%
  group_by(Sex) %>%
  summarise(mean(body_kg))

t.test(body_kg ~ Sex, data = back)

## 
##  Welch Two Sample t-test
## 
## data:  body_kg by Sex
## t = -7.0863, df = 77.002, p-value = 5.704e-10
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -20.32511 -11.40803
## sample estimates:
## mean in group Female   mean in group Male 
##             62.28236             78.14893

p-value меньше .05, поэтому мы можем отклонить нулевую гипотезу о том, что масса студентов-мужчин и студентов-женщин одинаковая. Мы принимаем альтернативную гипотезу о различии средних в генеральной совокупности.

Визуализируйте распределение этих двух переменных в зависимости от пола (используя ggplot2)

library(ggplot2)
ggplot(back)+
  geom_histogram(aes(x = body_kg, fill = Sex), bins = 15, position = "identity", alpha = 0.7)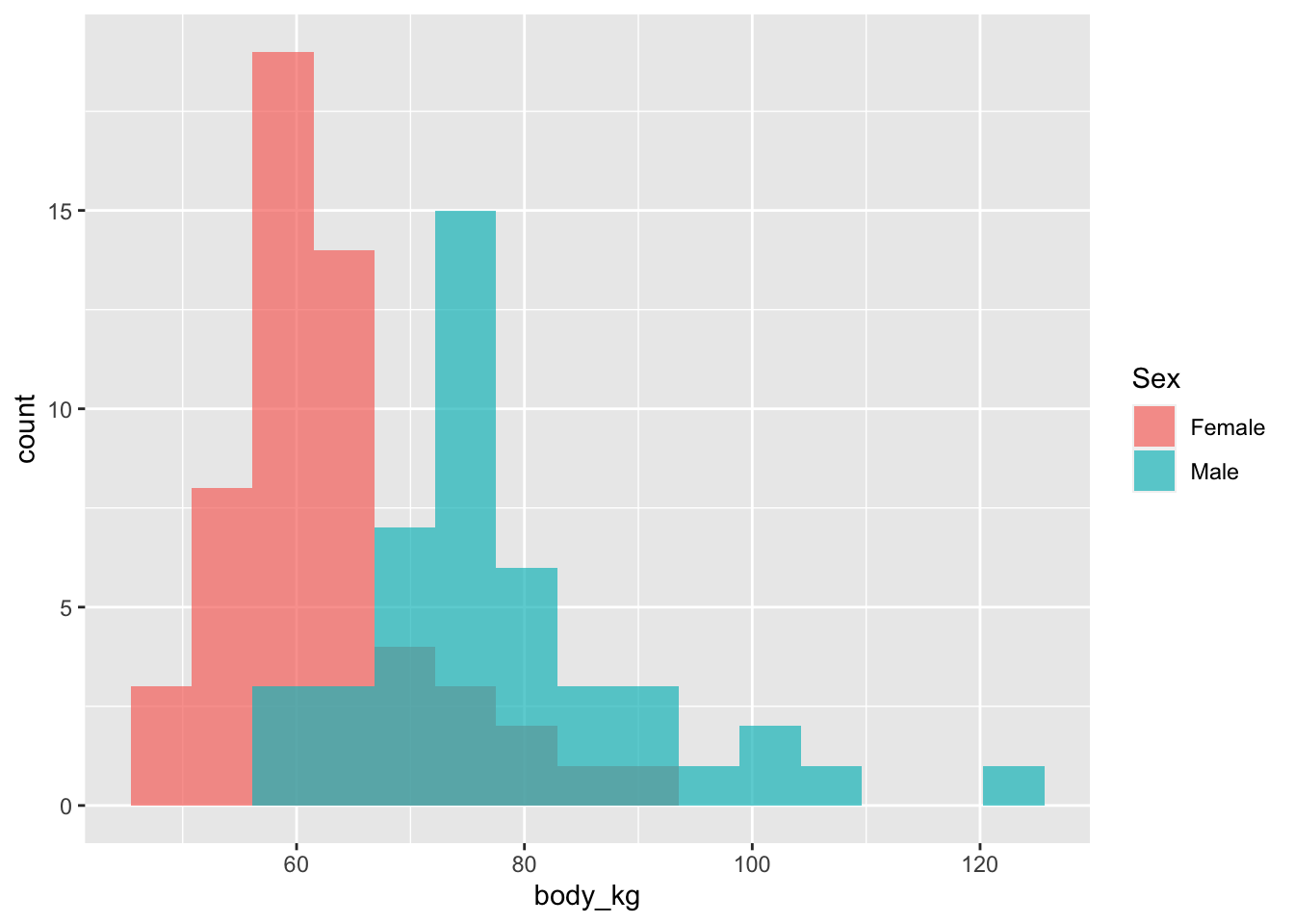

Постройте диаграмму рассеяния с помощью ggplot2. Цветом закодируйте пол респондента.

ggplot(back, aes(x = body_kg, y = backpack_kg))+
  geom_point(aes(colour = Sex), alpha = 0.5, size = 2)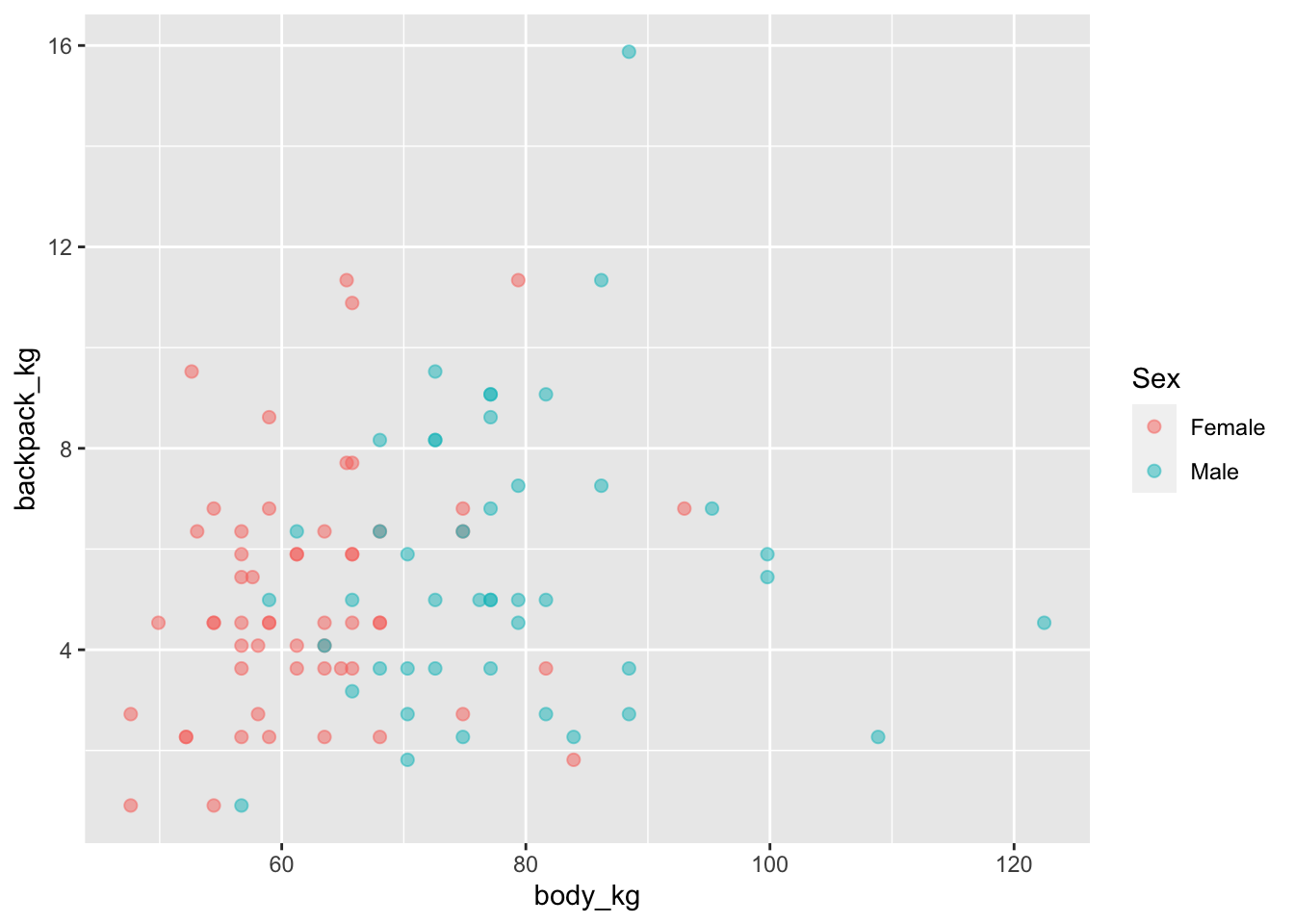

20.31 Ковариация

Посчитайте матрицу ковариаций для веса студентов и их рюкзаков в фунтах. Различаются ли результаты подсчета ковариации этих двух переменных от результатов подсчета ковариаций веса студентов и их рюкзаков в килограммах? Почему?

back %>%
  select(BodyWeight, BackpackWeight) %>%
  cov()

##                BodyWeight BackpackWeight
## BodyWeight      864.20960       32.08788
## BackpackWeight   32.08788       33.23677

Результаты различаются, потому что значение ковариации зависит от размерности исходных шкал.

20.32 Коэффициент корреляции

Посчитайте коэффициент корреляции Пирсона для веса студентов и их рюкзаков в фунтах. Различаются ли результаты подсчета коэффициента корреляции Пирсона (сам коэффициент, p-value) этих двух переменных от результатов подсчета корреляции Пирсона веса студентов и их рюкзаков в килограммах? Почему?

cor.test(back$BackpackWeight, back$BodyWeight)

## 
##  Pearson's product-moment correlation
## 
## data:  back$BackpackWeight and back$BodyWeight
## t = 1.9088, df = 98, p-value = 0.05921
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.007360697  0.371918344
## sample estimates:
##       cor 
## 0.1893312

Результаты не различаются, потому что значение ковариации не зависит от размерности исходных шкал.

Посчитайте коэффициент корреляции Пирсона для веса и роста супергероев из датасета heroes. Проинтерпретируйте результат.

cor.test(heroes$Weight, heroes$Height)

## 
##  Pearson's product-moment correlation
## 
## data:  heroes$Weight and heroes$Height
## t = 4.3555, df = 488, p-value = 1.619e-05
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.1066877 0.2772717
## sample estimates:
##       cor 
## 0.1934412

p-value меньше 0.05, поэтому мы можем отклонить нулевую гипотезу об отсутствии линейной связи между ростом и весом и принять альтернативную гипотезу о том, что такая связь есть. Судя по знаку и размеру корреляции, чем выше рост, тем выше вес супергероя, но эта связь достаточно слабая.

Теперь посчитайте коэффициент корреляции Спирмена и коэффициент корреляции Кэнделла для веса и роста супергероев из датасета heroes. Различаются ли результаты по сравнению с коэффициентом корреляции Пирсона? Почему?

cor.test(heroes$Weight, heroes$Height, method = "spearman")

## 
##  Spearman's rank correlation rho
## 
## data:  heroes$Weight and heroes$Height
## S = 3915061, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.8003344

cor.test(heroes$Weight, heroes$Height, method = "kendall")

## 
##  Kendall's rank correlation tau
## 
## data:  heroes$Weight and heroes$Height
## z = 21.548, p-value < 2.2e-16
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##       tau 
## 0.6751664

В обоих случаях p-value меньше 0.05, поэтому мы можем отклонить нулевую гипотезу об отсутствии связи между ростом и весом и принять альтернативную гипотезу о том, что такая связь есть. Сильное различие между коэффициентами корреляции указывает на нелинейность этой связи, либо же на наличие значительных выбросов в данных.

20 Решения заданий

20.1 Intro to R

20.2 Vectors creation

20.3 Coercion

20.4 Vectorisation

20.5 Indexing vectors

20.6 Missing values

20.7 Matrix

20.8 List

20.9 Датафрейм

20.10 Условные конструкции

20.11 Создание функций

20.12 Семейство функций apply()

20.13 magrittr::%>%

20.14 Columns selection: dplyr::select()

20.15 Rows selection: dplyr::slice() and dplyr::filter()

20.16 Rows sorting: dplyr::arrange()

20.17 Unique values: dplyr::distinct()

20.18 Making new columns: dplyr::mutate() and dplyr::transmute()

20.19 Агрегация: dplyr::group_by() %>% summarise()

20.20 Operations with several columns: across()

20.21 Merging dataframes: *_join {#solution_join}

20.22 Tidy data

20.23 Описательная статистика

20.24 Построение графиков в ggplot2

20.25 Распределения

20.26 Одновыборочный t-test

20.27 Двухвыборочный зависимый t-test

20.28 Двухвыборочный независимый t-test

20.29 Непараметрические аналоги t-теста

20.30 Исследование набора данных Backpack

20.31 Ковариация

20.32 Коэффициент корреляции

20.13 magrittr::`%>%`

20.14 Columns selection: `dplyr::select()`

20.15 Rows selection: `dplyr::slice()` and `dplyr::filter()`

20.16 Rows sorting: `dplyr::arrange()`

20.17 Unique values: `dplyr::distinct()`

20.18 Making new columns: `dplyr::mutate()` and `dplyr::transmute()`

20.19 Агрегация: `dplyr::group_by() %>% summarise()`

20.20 Operations with several columns: `across()`

20.24 Построение графиков в `ggplot2`