A <- matrix(1:20, nrow = 5, ncol = 4)
A [,1] [,2] [,3] [,4]
[1,] 1 6 11 16
[2,] 2 7 12 17
[3,] 3 8 13 18
[4,] 4 9 14 19
[5,] 5 10 15 20Давайте повторим то, что мы знаем про вектор в R:
Вектор – это последовательность из значений.
Порядок значений имеет значение, но этот порядок одномерный.
Внутри вектора могут быть данные только одного типа
Как вы уже поняли, вектор – это одно из важнейших понятий в R, и он нам будет встречаться дальше постоянно. Обычно работа с данными – это именно работа с векторами, различные операции на векторах.
Однако иногда в понятии вектора нам уже становится несколько тесно. Поэтому нам нужно выйти за рамки его ограничений. Во-первых, во второе (и дальнейшие) измерения – это делает матрица (matrix). Во-вторых, нам нужна структура, которая могла бы содержать данные разных типов – это список (list).
Если вдруг вас пугает это слово, то совершенно зря. Матрица (matrix) – это всего лишь “двумерный” вектор: вектор, у которого есть не только длина, но и ширина. Создать матрицу можно с помощью функции matrix() из вектора, указав при этом количество строк и столбцов.
A <- matrix(1:20, nrow = 5, ncol = 4)
A [,1] [,2] [,3] [,4]
[1,] 1 6 11 16
[2,] 2 7 12 17
[3,] 3 8 13 18
[4,] 4 9 14 19
[5,] 5 10 15 20Если мы знаем сколько значений в матрице и сколько мы хотим строк, то количество столбцов указывать необязательно:
A <- matrix(1:12, nrow = 4)
A [,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12Все остальное так же как и с векторами: внутри находится данные только одного типа. Поскольку матрица – это уже двумерный массив, то у него имеется два индекса. Эти два индекса разделяются запятыми.
A[2, 3][1] 10Первый индекс – выбор строк, второй индекс – выбор колонок1. Результат – пересечение выбранных строк и столбцов.
Так же как и с векторами, матрицы можно индексировать числовыми векторами:
A[1:2, 2:3] [,1] [,2]
[1,] 5 9
[2,] 6 10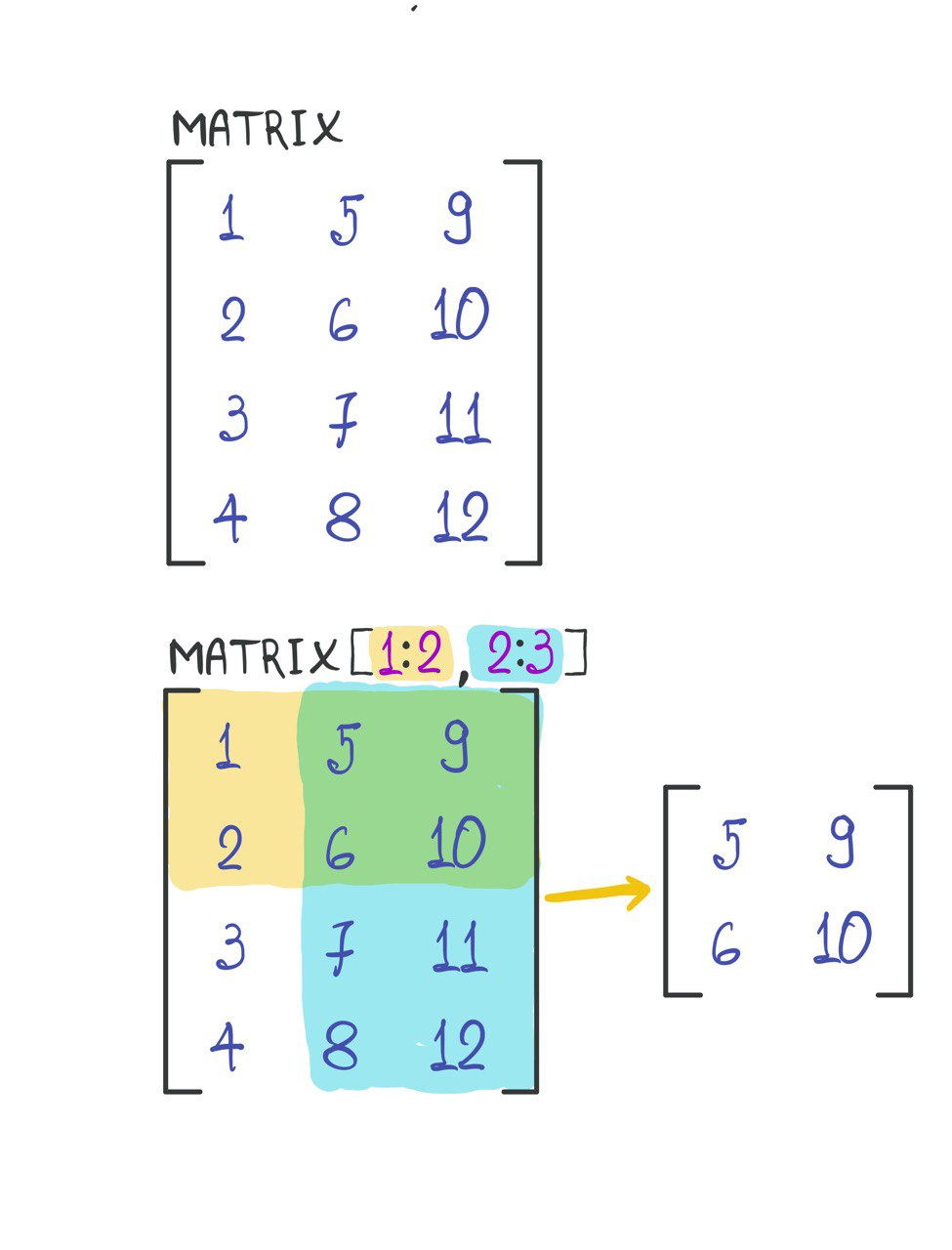
И даже логическими матрицами (матрицы имеют такие же типы, как и вектора):
A[A > 10][1] 11 12В этом случае матрица упростится до вектора.
Если же мы оставляем пустое поле вместо числа, то мы выбираем все строки/колонки в зависимости от того, оставили мы поле пустым до или после запятой:
A[, 2:3] [,1] [,2]
[1,] 5 9
[2,] 6 10
[3,] 7 11
[4,] 8 12A[1:2, ] [,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10A[, ] [,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12Так же как и в случае с обычными векторами, часть матрицы можно переписать:
A[1:2, 1:2] <- 100
A [,1] [,2] [,3]
[1,] 100 100 9
[2,] 100 100 10
[3,] 3 7 11
[4,] 4 8 12В принципе, это все, что нам нужно знать о матрицах. Матрицы используются в R довольно редко, особенно по сравнению, например, с MATLAB. Но вот индексировать матрицы хорошо бы уметь: это понадобится в работе с датафреймами (см. Глава 4.4).
Два измерения – это не предел! Структура с одним типом данных внутри, но с тремя измерениями или больше, называется массивом (array). Создание массива очень похоже на создание матрицы: задаем вектор, из которого будет собран массив, и размерность массива.
array_3d <- array(1:12, c(3, 2, 2))
array_3d, , 1
[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
, , 2
[,1] [,2]
[1,] 7 10
[2,] 8 11
[3,] 9 12Теперь представим себе вектор без ограничения на одинаковые данные внутри. И получим список (list)!
simple_list <- list(42, "Пам пам", TRUE)
simple_list[[1]]
[1] 42
[[2]]
[1] "Пам пам"
[[3]]
[1] TRUEА это значит, что там могут содержаться самые разные данные, в том числе и другие списки, векторы и матрицы (и другие объекты, которые нам еще не знакомы)!
complex_list <- list(c("Wow", "this", "list", "is", "so", "big"), "16", simple_list, A)
complex_list[[1]]
[1] "Wow" "this" "list" "is" "so" "big"
[[2]]
[1] "16"
[[3]]
[[3]][[1]]
[1] 42
[[3]][[2]]
[1] "Пам пам"
[[3]][[3]]
[1] TRUE
[[4]]
[,1] [,2] [,3]
[1,] 100 100 9
[2,] 100 100 10
[3,] 3 7 11
[4,] 4 8 12Если у нас сложный список, то есть очень классная функция str(), чтобы посмотреть, как он устроен:
str(complex_list)List of 4
$ : chr [1:6] "Wow" "this" "list" "is" ...
$ : chr "16"
$ :List of 3
..$ : num 42
..$ : chr "Пам пам"
..$ : logi TRUE
$ : num [1:4, 1:3] 100 100 3 4 100 100 7 8 9 10 ...Представьте, что список - это такое дерево с ветвистой структурой. А на конце этих ветвей - листья-векторы.
Как и в случае с векторами мы можем давать имена элементам списка:
named_list <- list(name = "Veronika", age = 26, student = FALSE)
named_list$name
[1] "Veronika"
$age
[1] 26
$student
[1] FALSEК списку можно обращаться как с помощью индексов, так и по именам. Начнем с последнего:
named_list$age[1] 26А вот с индексами сложнее, и в этом очень легко запутаться. Давайте попробуем сделать так, как мы делали это раньше:
named_list[1]$name
[1] "Veronika"Мы, по сути, получили элемент списка – просто как часть списка, т.е. как список длиной один:
class(named_list)[1] "list"class(named_list[1])[1] "list"А вот чтобы добраться до самого элемента списка (и сделать с ним что-то хорошее), нам нужна не одна, а две квадратных скобочки:
named_list[[1]][1] "Veronika"class(named_list[[1]])[1] "character"Как и в случае с вектором, к элементу списка можно обращаться по имени. Здесь тоже будет иметь значение, одинарные или двойные квадратные скобки вы используете:
named_list["age"]$age
[1] 26named_list[["age"]][1] 26Хотя последнее – практически то же самое, что и использование знака $.

Итак, мы перешли к самому главному. Самому-самому. Датафреймы (dataframes). Более того, сейчас станет понятно, зачем нам нужно было разбираться со всеми предыдущими темами.
Без векторов мы не смогли бы разобраться с матрицами и списками. А без последних мы не сможем понять, что такое датафрейм.
Представьте себе, что мы хотим записать различную информацию о нескольких респондентах. Мы могли бы записать это в список из векторов.
list(name = c("Veronika", "Eugeny", "Lena", "Misha", "Sasha"),
age = c(26, 34, 23, 27, 26),
student = c(FALSE, FALSE, TRUE, TRUE, TRUE))$name
[1] "Veronika" "Eugeny" "Lena" "Misha" "Sasha"
$age
[1] 26 34 23 27 26
$student
[1] FALSE FALSE TRUE TRUE TRUEДатафрейм очень похож на список. Просто поменяем в команде выше list() на data.frame() и посмотрим, что изменится:
df <- data.frame(name = c("Veronika", "Eugeny", "Lena", "Misha", "Sasha"),
age = c(26, 34, 23, 27, 26),
student = c(FALSE, FALSE, TRUE, TRUE, TRUE))
str(df)'data.frame': 5 obs. of 3 variables:
$ name : chr "Veronika" "Eugeny" "Lena" "Misha" ...
$ age : num 26 34 23 27 26
$ student: logi FALSE FALSE TRUE TRUE TRUEdf name age student
1 Veronika 26 FALSE
2 Eugeny 34 FALSE
3 Lena 23 TRUE
4 Misha 27 TRUE
5 Sasha 26 TRUEВообще, очень похоже на список, не правда ли? Так и есть, датафрейм – это что-то вроде проименованного списка, каждый элемент которого является atomic вектором фиксированной длины. Скорее всего, вы представляли список “горизонтально”. Если это так, то теперь “переверните” список у себя в голове на 90 градусов. Так, чтобы названия векторов оказались сверху, а элементы списка стали столбцами.
Поскольку длина всех этих векторов одинаковая (обязательное условие!), то данные представляют собой табличку, похожую на матрицу. Но в отличие от матрицы, разные столбцы могут иметь разные типы данных. В нашем случае первая колонка – character, вторая колонка – numeric, третья колонка – logical. Тем не менее, обращаться с датафреймом можно и как с проименованным списком, и как с матрицей:
df$age[1] 26 34 23 27 26Здесь мы сначала извлекли колонку age с помощью оператора $. Результатом этой операции является числовой вектор. Колонки датафрейма – это и есть векторы!
df$age[2:3][1] 34 23Теперь с ним можно работать как с обычным вектором: мы вытащили кусок, выбрав индексы 2 и 3.
Используя оператор $ и присваивание можно создавать новые колонки датафрейма:
df$lovesR <- TRUE #правило recycling - узнали? согласны?
df name age student lovesR
1 Veronika 26 FALSE TRUE
2 Eugeny 34 FALSE TRUE
3 Lena 23 TRUE TRUE
4 Misha 27 TRUE TRUE
5 Sasha 26 TRUE TRUEНу а можно просто обращаться с помощью двух индексов через запятую, как мы это делали с матрицей:
df[3:5, 2:3] age student
3 23 TRUE
4 27 TRUE
5 26 TRUEКак и с матрицами, первый индекс означает строчки, а второй – столбцы.
А еще можно использовать названия колонок внутри квадратных скобок:
df[1:2, "age"][1] 26 34df[1:2, c("age", "name")] age name
1 26 Veronika
2 34 EugenyИ здесь перед нами открываются невообразимые возможности! Узнаем, любят ли R те, кто моложе среднего возраста в группе:
df[df$age < mean(df$age), 4][1] TRUE TRUE TRUE TRUEОбратите внимание, как удобно нам здесь пригодилось то, что мы научились делать с векторами (Глава 3). Сначала мы посчитали среднее значение абсолютно так же, как мы делали это с векторами:
mean(df$age)[1] 27.2Полученное среднее поэлементно сравнили с каждым значением колонки (т.е. вектора) df$age:
df$age < mean(df$age)[1] TRUE FALSE TRUE TRUE TRUEМы получили логический вектор, длина которого совпадает с длиной датафрейма. При этом TRUE стоит на тех позициях, где в соответствующей строчке в датафрейме возраст респондента больше среднего, а FALSE – в остальных случаях. Теперь этот логический вектор мы используем для выбора строк в исходном датафрейме:
df[df$age < mean(df$age), ] name age student lovesR
1 Veronika 26 FALSE TRUE
3 Lena 23 TRUE TRUE
4 Misha 27 TRUE TRUE
5 Sasha 26 TRUE TRUEНаконец, тут же мы можем вытащить нужные колонки, по номеру колонки или ее названию:
df[df$age < mean(df$age), 4][1] TRUE TRUE TRUE TRUEЭту же задачу можно выполнить другими способами:
df$lovesR[df$age < mean(df$age)][1] TRUE TRUE TRUE TRUEdf[df$age < mean(df$age), 'lovesR'][1] TRUE TRUE TRUE TRUEВ большинстве случаев подходят сразу несколько способов – тем не менее, стоит овладеть ими всеми. Чем богаче ваш арсенал инструментов работы в R, тем легче вам обрабатывать свои данные: возможность сделать одно и то же действие добавляет вам гибкости, потому что разные способы будут более или менее подходящими в разных ситуациях.
Датафреймы удобно просматривать в RStudio. Для это нужно написать команду View(df) или же просто нажать на названии нужной переменной из списка вверху справа (там где Environment). Тогда увидите табличку, очень похожую на Excel и тому подобные программы для работы с таблицами. Там же есть и всякие возможности для фильтрации, сортировки и поиска 2.
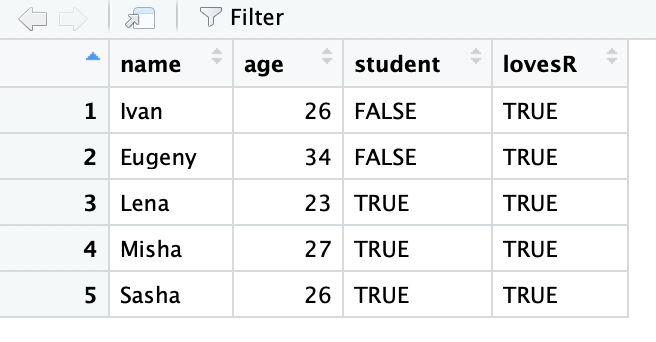
Но, конечно, интереснее все эти вещи делать руками, т.е. с помощью написания кода.
Датафреймы – это структура, которая будет встречаться вам чаще всего при работе с данными в R. С одной стороны, кажется, что она все равно довольно ограниченная: в каждой колонке должно быть одинаковое количество значений, внутри колонки только один тип данных. Но именно так обычно и представлены наши данные. Например, если вы загрузите результаты опроса Google Forms в виде таблицы, то каждая строчка будет респондентом, а каждая колонка – ответом на какой-то вопрос. Поэтому количество значений в каждой колонке будет одинаковым (хотя значения могут быть пропущенными), а каждая колонка – имеет свой тип. Например, год рождения – и это должна быть числовая колонка, с которой вы сможете делать все, что вы умеете делать с числовыми колонками. Например, посчитать возраст. Если в колонке с годом рождения оказалось что-то кроме чисел, то это повод для исследования данных.
…
Формулы – это специальный класс в R, который используется в первую очередь для статистических моделей.
Выглядит формула следующим образом:
y ~ xy ~ xclass(y ~ x)[1] "formula"Как видите, здесь нет никаких кавычек, т.е. это не строковое значение, а отдельный класс. В каждой формуле должна быть тильда (~), которая имеет смысл знака равно (=) в уравнениях (например, для уравнений линейной регрессии). Слева от ~ обычно находится зависимая переменная, а справа – независимые (предикторы).
Кроме статистических моделей, формулы используются много где как служебная конструкция, чтобы задать соответствующие пары значений. Вот несколько примеров:
Это универсальный порядок: что в других языках программирования, что в линейной алгебре первый индекс – выбор строчек, второй индекс – выбор столбцов.↩︎
Все, что вы нажмете в этом окошке, никак не повлияет на исходную переменную. Так что можете смело использовать эти функции для исследования содержимого датафрейма.↩︎