library(tidyverse)
library(palmerpenguins)
penguins <- penguins %>%
drop_na(bill_length_mm:body_mass_g)
penguins %>%
select(bill_length_mm:body_mass_g) %>%
plot(col = penguins$species)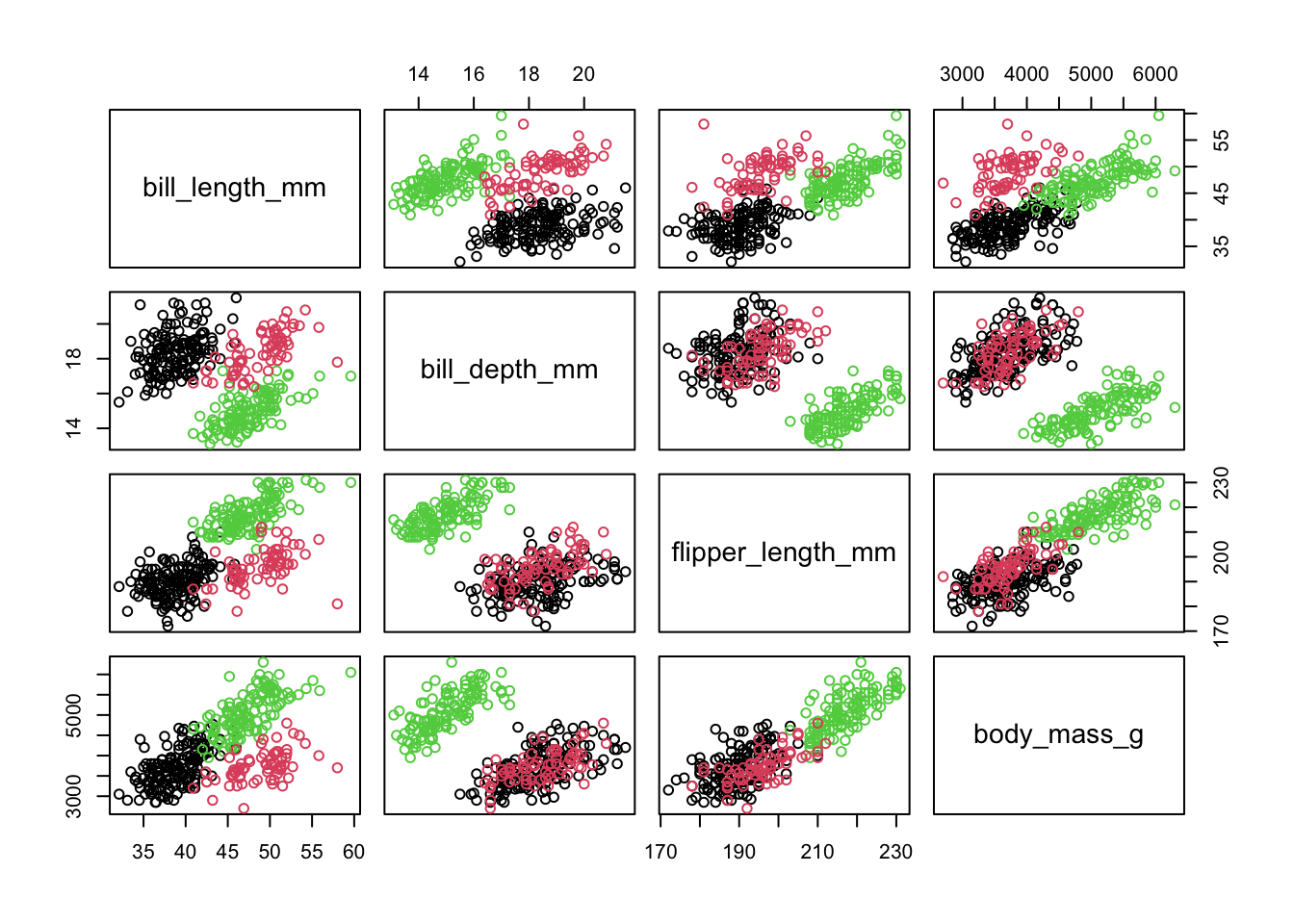
24 Многомерные методы анализа данных
И.С. Поздняков 
Многомерные методы анализа данных – методы работы с данными, в которых много колонок. Мы уже сталкивались с некоторыми многомерными методами, например, с множественной линейной регрессией (Глава 21.5). Поэтому вы знаете, что многомерность создает новые проблемы. Например, при множественных корреляциях или попарных сравнениях возникает проблема множественных сравнений, а при использовании множественной регрессии лишние предикторы могут ловить только шум и приводить к переобучению (если говорить в терминах машинного обучения). Короче говоря, больше - не значит лучше. Нужно четко понимать, зачем мы используем данные и что пытаемся измерить.
Однако в некоторых случаях мы в принципе не можем ничего интересного сделать с маленьким набором переменных. Много ли мы можем измерить личностным тестом с одним единственным вопросом? Можем ли мы точно оценить уровень интеллекта по успешности выполнения одного единственного задания? Очевидно, что нет. Более того, даже концепция интеллекта в современном его представлении появилась во многом благодаря разработке многомерных методов анализа! Ну или наоборот: исследования интеллекта подстегнули развитие многомерных методов.
24.1 Уменьшение размерности
Представьте многомерное пространство, где каждая колонка — это отдельная ось, а каждая строка задает координаты одной точки в этом пространстве. Мы получим многомерную диаграмму рассеяния.
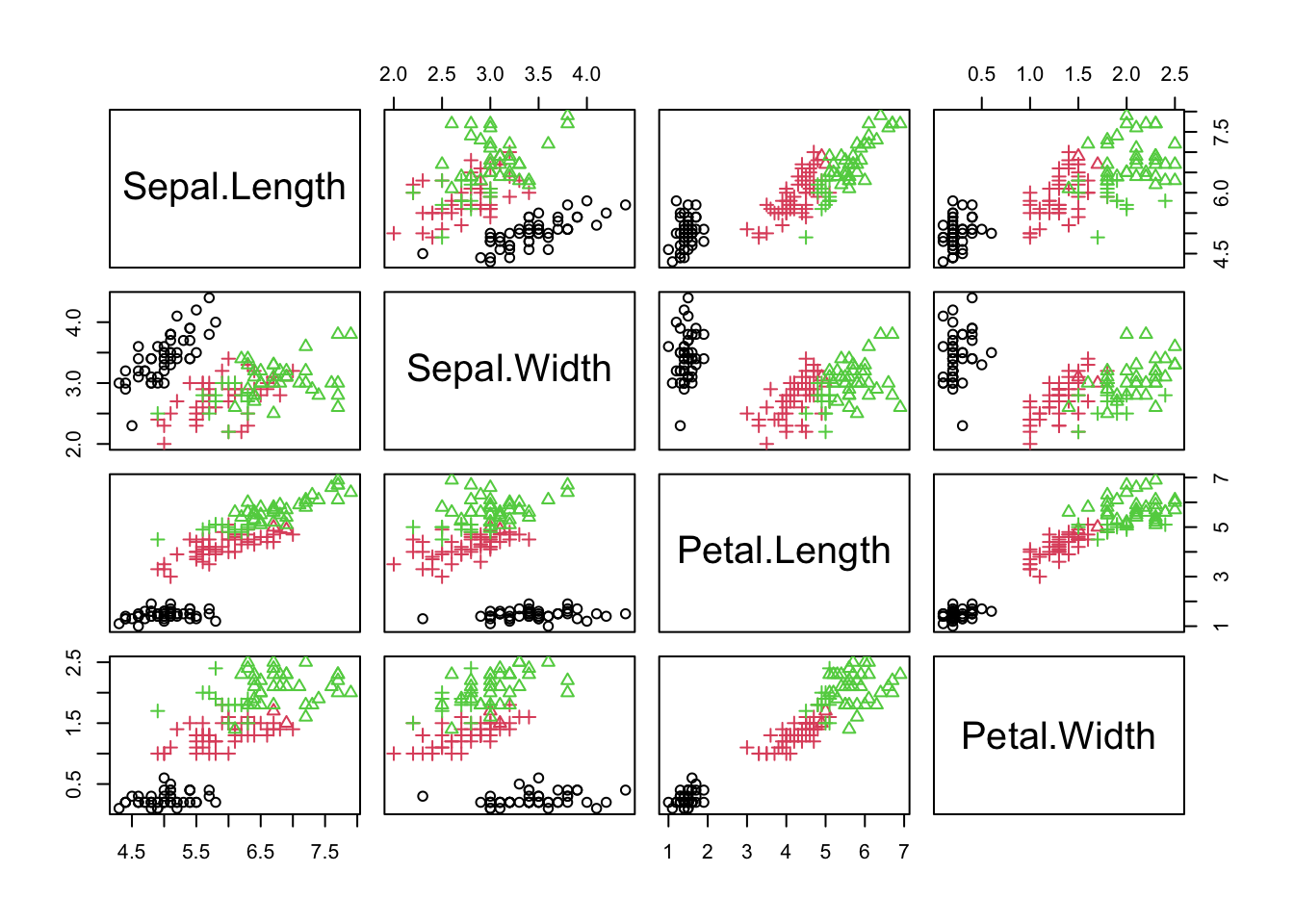
Многомерную диаграмму рассеяния, к сожалению, нельзя нарисовать, поэтому нарисуем несколько двухмерных диаграмм рассеяния для отображения сочетания всех колонок со всеми набора данных penguins.
Даже представить как устроены многомерные данные очень трудно, а ведь мы отобразили только четыре числовых колонки! Понять связи между отдельными переменными мы можем, если посмотрим на каждую диаграмму рассеяния по отдельности, но и то если их не слишком много. Но связи в многомерных данных могут быть гораздо более сложными и на простых диаграммах рассеяния их иногда нельзя заметить. Это как смотреть на тени, поворачивая какой-нибудь предмет различными сторонами.
Уменьшение размерности позволяет вытащить из данных самую мякотку, уместив исходные данные в небольшое количество переменных. Остальное из данных удаляется.
Данные сниженной размерности гораздо проще визуализировать. Например, снизив размерность данных до двух шкал, можно просто нарисовать диаграмму рассеяния. Анализируя связь полученных шкал с изначальными шкалами и взаимное расположение точек в новых шкалах, можно многое понять об исследуемых данных.
Однако снижение размерности используется не только для эксплораторного анализа, но и для снижения количества фичей в машинном обучения, для удаления шума из данных, для более экономного хранения данных и многих других задач.
24.2 Анализ главных компонент (Principal component analysis)
Анализ главных компонент (АГК; Principal component analysis) – это, пожалуй, самый известный метод уменьшения размерности. АГК просто поворачивает систему координат многомерного пространства, которое задано имеющимися числовыми колонками. Координатная система поворачивается таким образом, чтобы первые оси объясняли как можно больший разброс данных, а последние - как можно меньший. Тогда мы могли бы отбросить последние оси и не очень-то многое потерять в данных. Для двух осей это выглядит вот так:
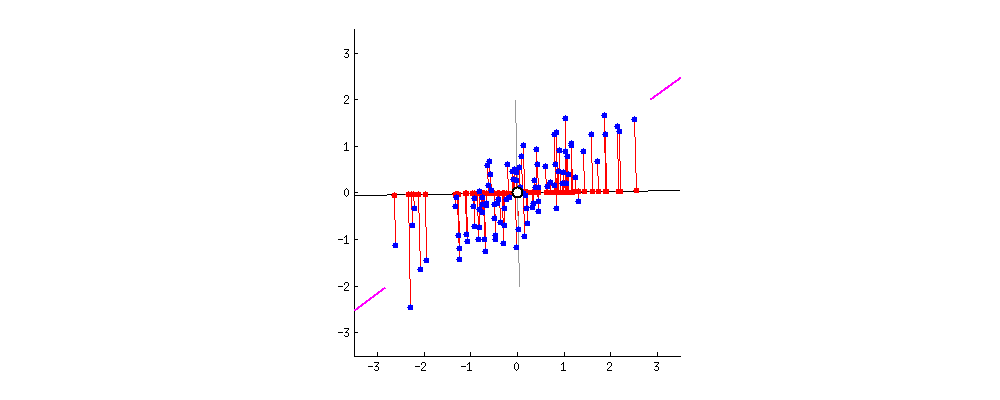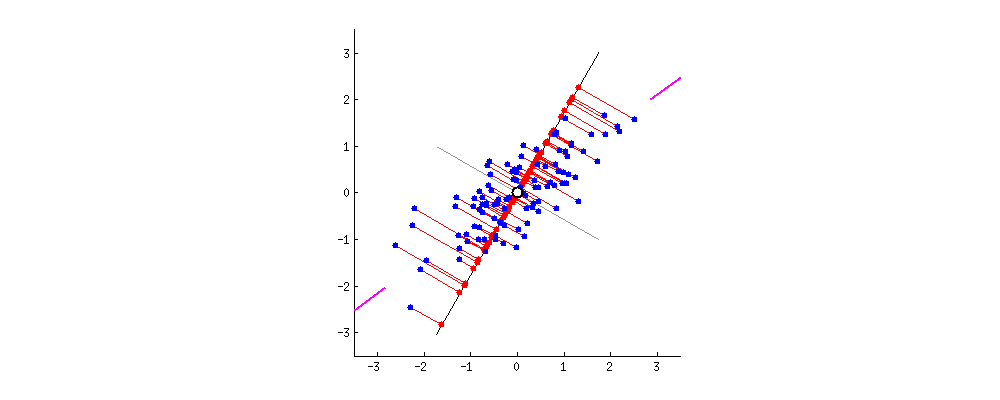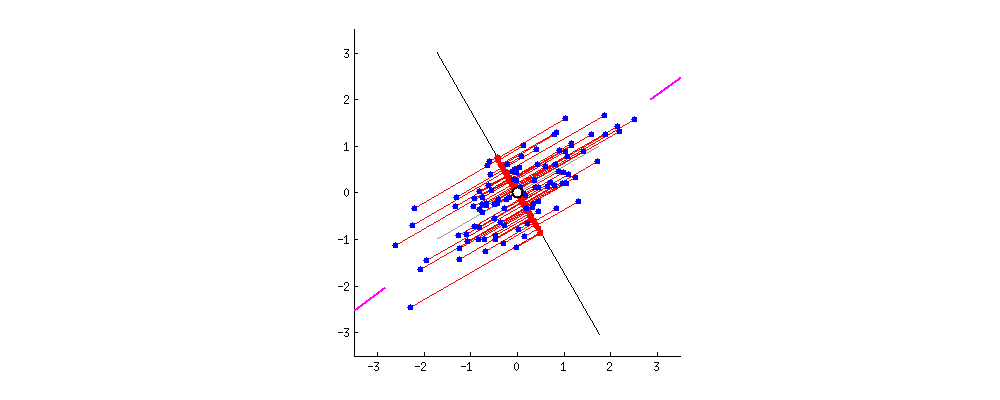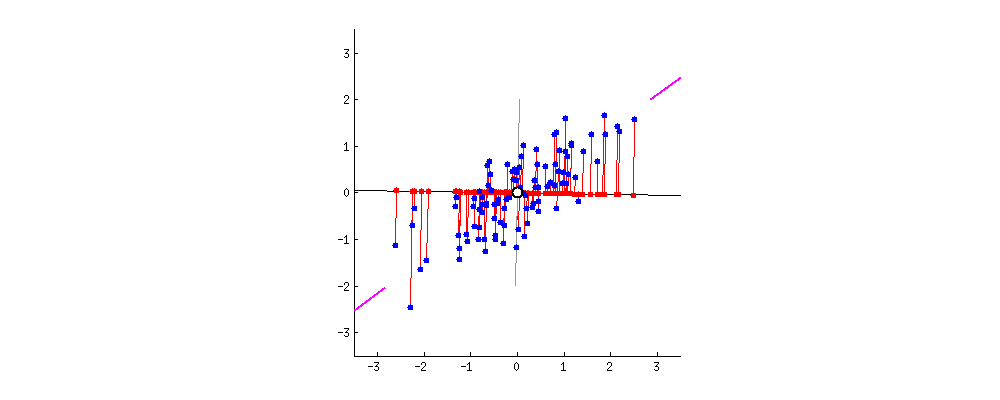
Первая ось должна минимизировать красные расстояния. Вторая ось будет просто перпендикулярна первой оси.
Итак, для начала нам нужно центрировать и нормировать данные - вычесть среднее и поделить на стандартное отклонение, т.е. посчитать \(z\)-оценки (см. Глава 12.5.3.1). Это нужно для того, чтобы сделать все шкалы равноценными. Это особенно важно делать когда разные шкалы используют несопоставимые единицы измерения. Скажем, одна колонка - это масса человека в килограммах, а другая - рост в метрах. Если применять АГК на этих данных, то ничего хорошего не выйдет: вклад роста будет слишком маленьким. А вот если мы сделаем \(z\)-преобразование, то приведем и вес, и рост к “общему знаменателю”.
В базовом R уже есть инструменты для АГК princomp() и prcomp(), считают они немного по-разному. Возьмем более рекомендуемый вариант, prcomp(). Эта функция умеет самостоятельно поводить \(z\)-преобразования, для чего нужно поставить center = TRUE и scale. = TRUE.
penguins_prcomp <- penguins %>%
select(bill_length_mm:body_mass_g) %>%
prcomp(center = TRUE, scale. = TRUE)Уже много раз встречавшаяся нам функция summary(), примененная на результат проведения АГК, выдаст информацию о полученных компонентах. Наибольший интерес представляют строчки “Proportion of Variance” (доля дисперсии, объясненная компонентой) и “Cumulative Proportion” (накопленная доля дисперсии для компоненты данной и всех предыдущих компонент).
summary(penguins_prcomp)Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.6594 0.8789 0.60435 0.32938
Proportion of Variance 0.6884 0.1931 0.09131 0.02712
Cumulative Proportion 0.6884 0.8816 0.97288 1.00000Функция plot() повзоляет визуализировать соотношение разных компонент.
plot(penguins_prcomp)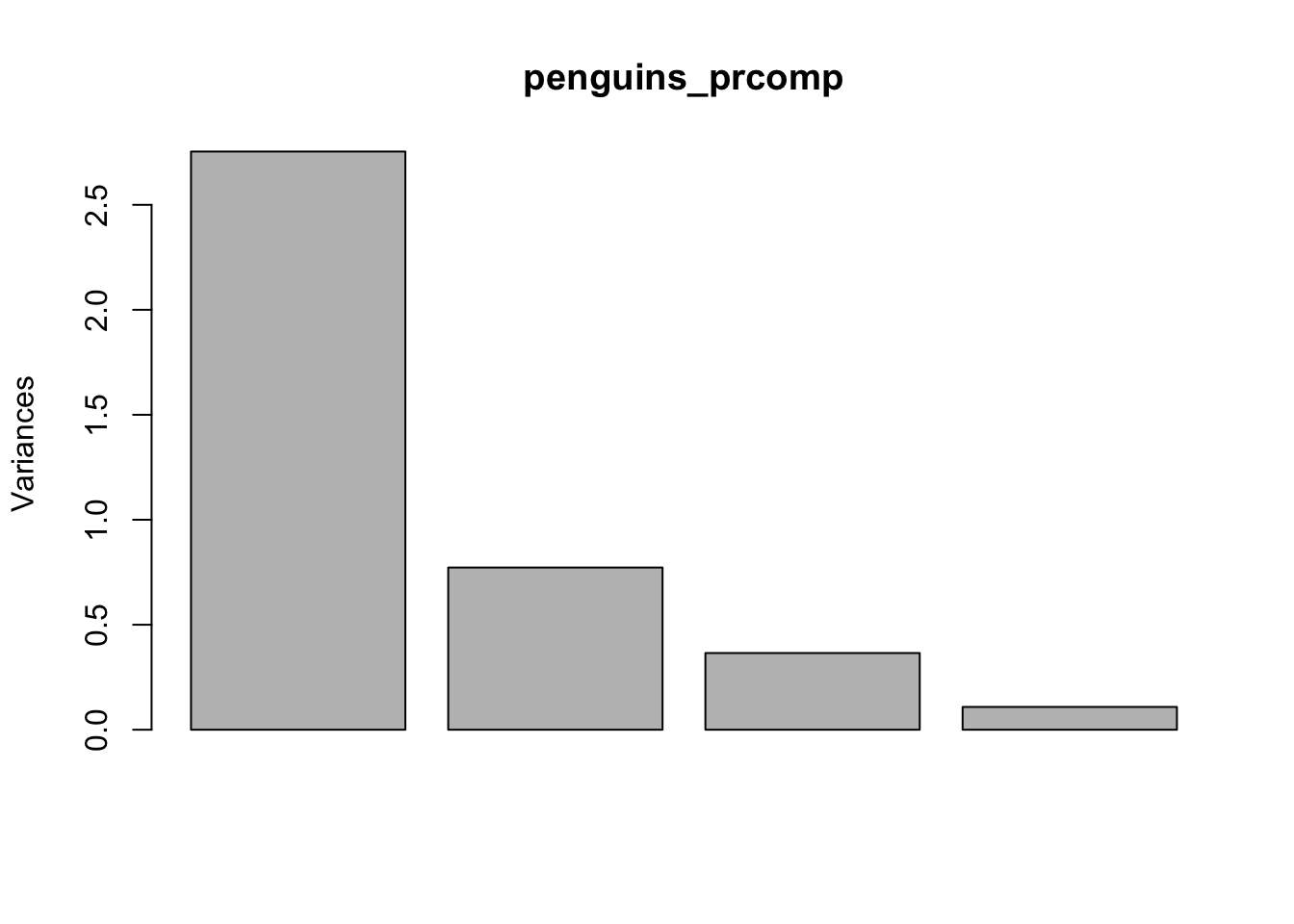
Как мы видим, первый компонент объясняет большую часть дисперсии, второй и третий компоненты заметно меньше, последний – совсем немного, скорее всего, этот компонент репрезентирует некоторый шум в данных.
Теперь мы можем визуализировать первые два компонента. Это можно сделать с помощью базовых инструментов R.
plot(penguins_prcomp$x[,1:2], col=penguins$species)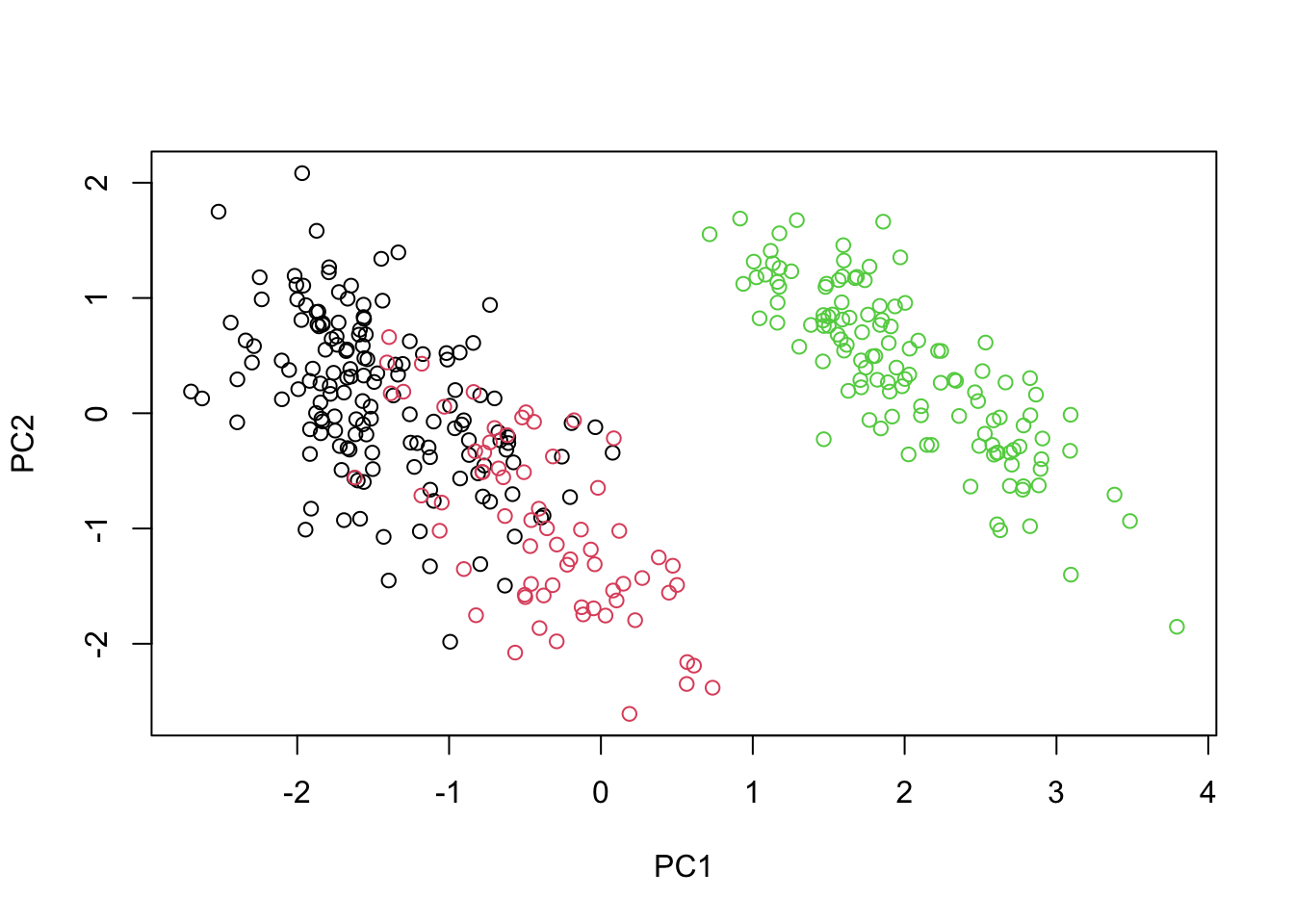
Однако пакет {factoextra} представляет гораздо более широкие возможности для визуализации.
install.packages("factoextra")Во-первых, как и с помощью базового plot(), можно нарисовать диаграмму рассеяния. Для этого воспользуемся функцией fviz_pca_ind():
library(factoextra)Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBafviz_pca_ind(penguins_prcomp)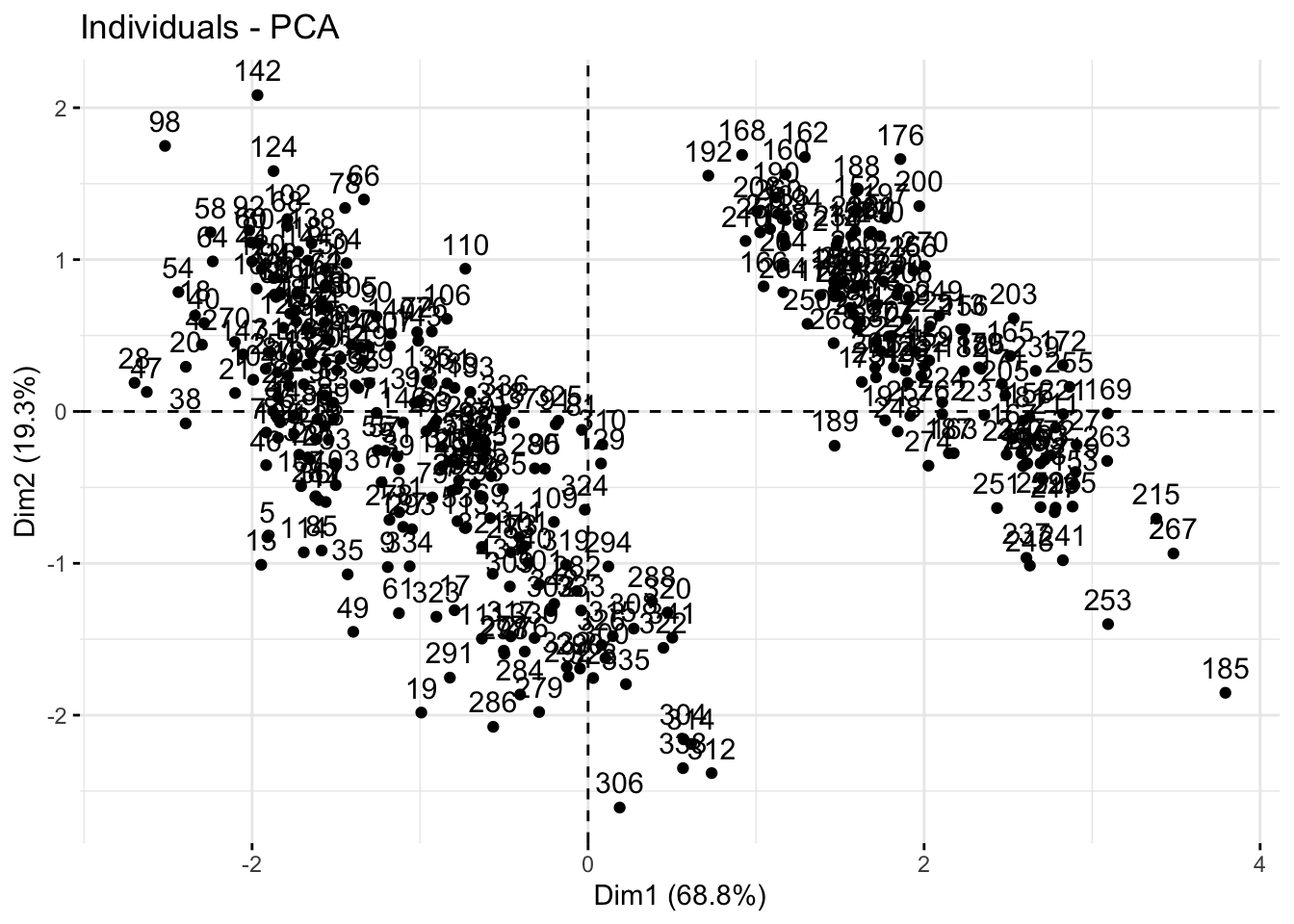
Параметром axes = можно выбрать нужные компоненты для отображения.
fviz_pca_ind(penguins_prcomp,
axes = c(3, 4))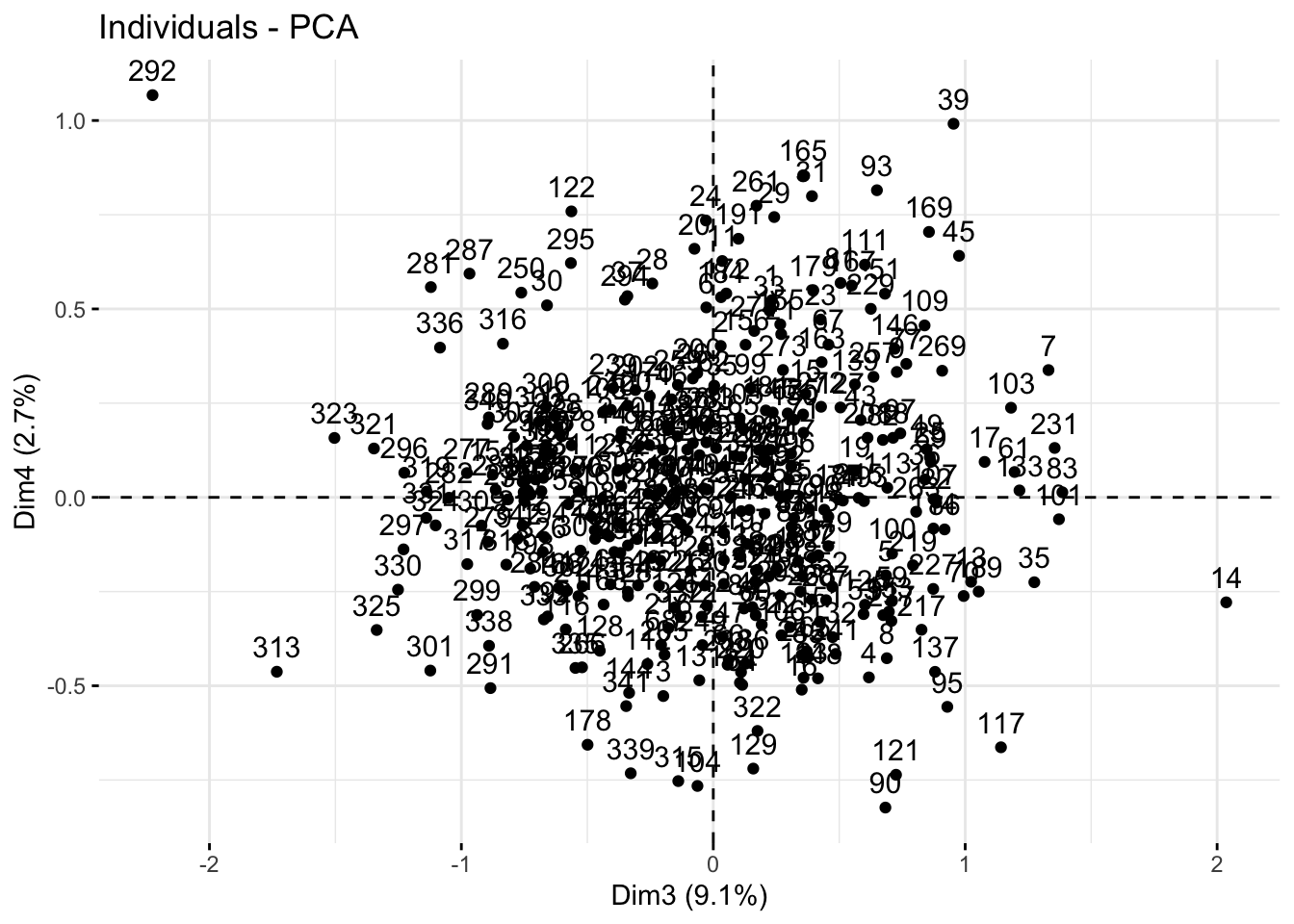
Добавить расцветку можно с помощью параметра habillage =, в которой надо подставить нужный вектор из изначальных данных.
fviz_pca_ind(penguins_prcomp,
habillage = penguins$species)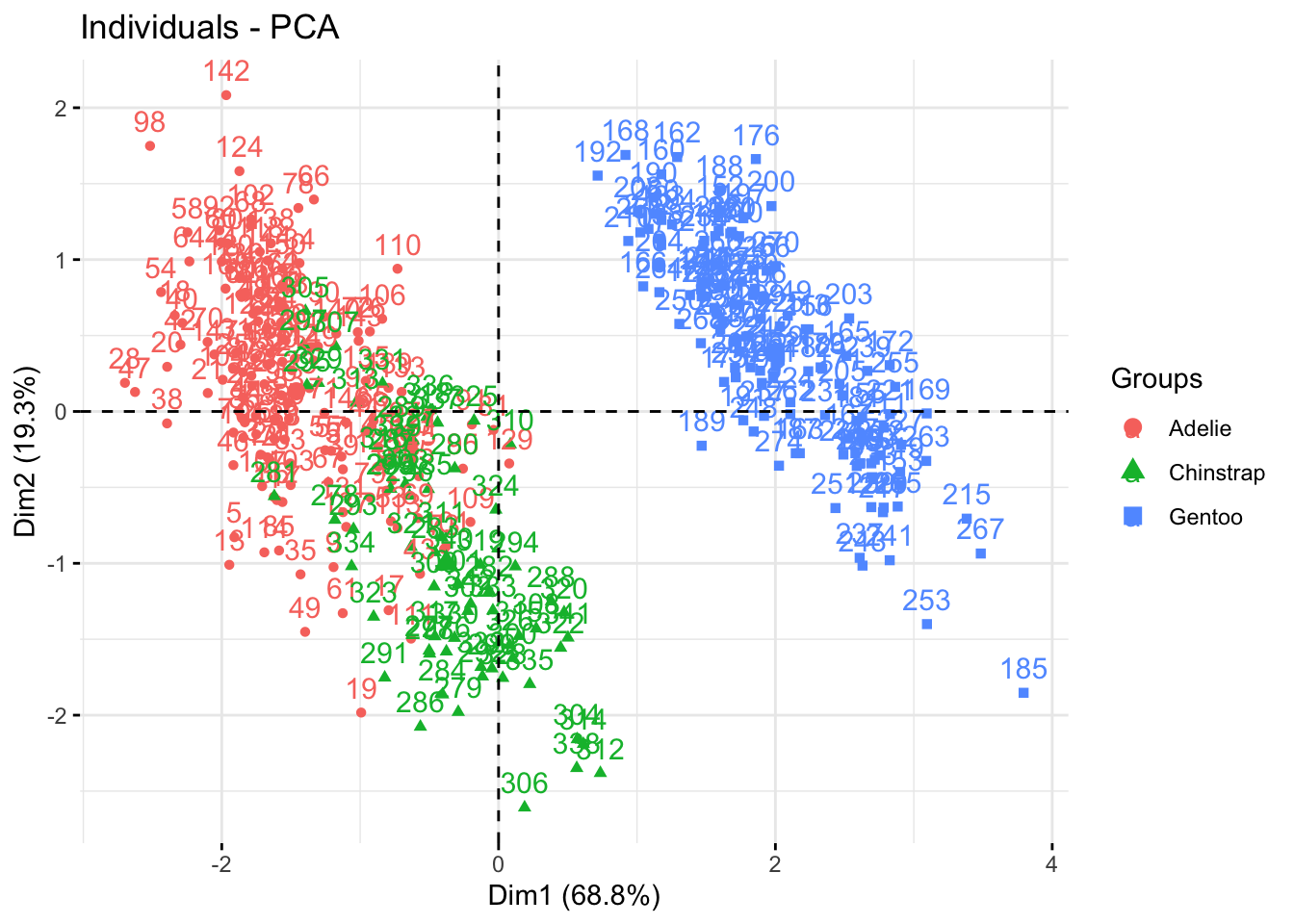
Параметр addEllipses = TRUE позволяет обрисовать эллипсы вокруг точек, если те раскрашены по группам с помощью habillage =.
fviz_pca_ind(penguins_prcomp,
habillage = penguins$species,
addEllipses = TRUE)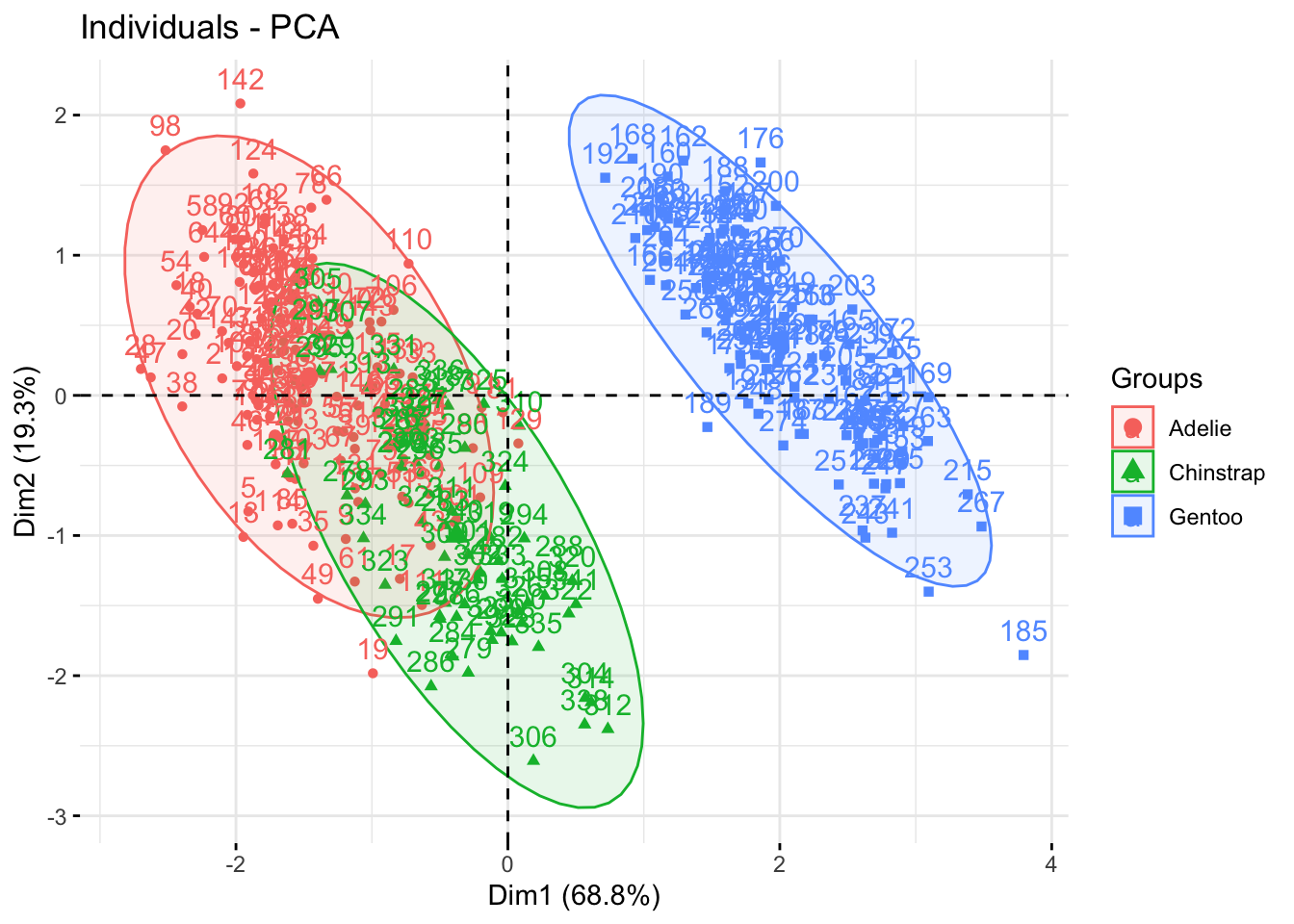
Чтобы рассмотреть отдельные точки, можно поставить repel = TRUE:
fviz_pca_ind(penguins_prcomp,
habillage = penguins$species,
addEllipses = TRUE,
repel = TRUE)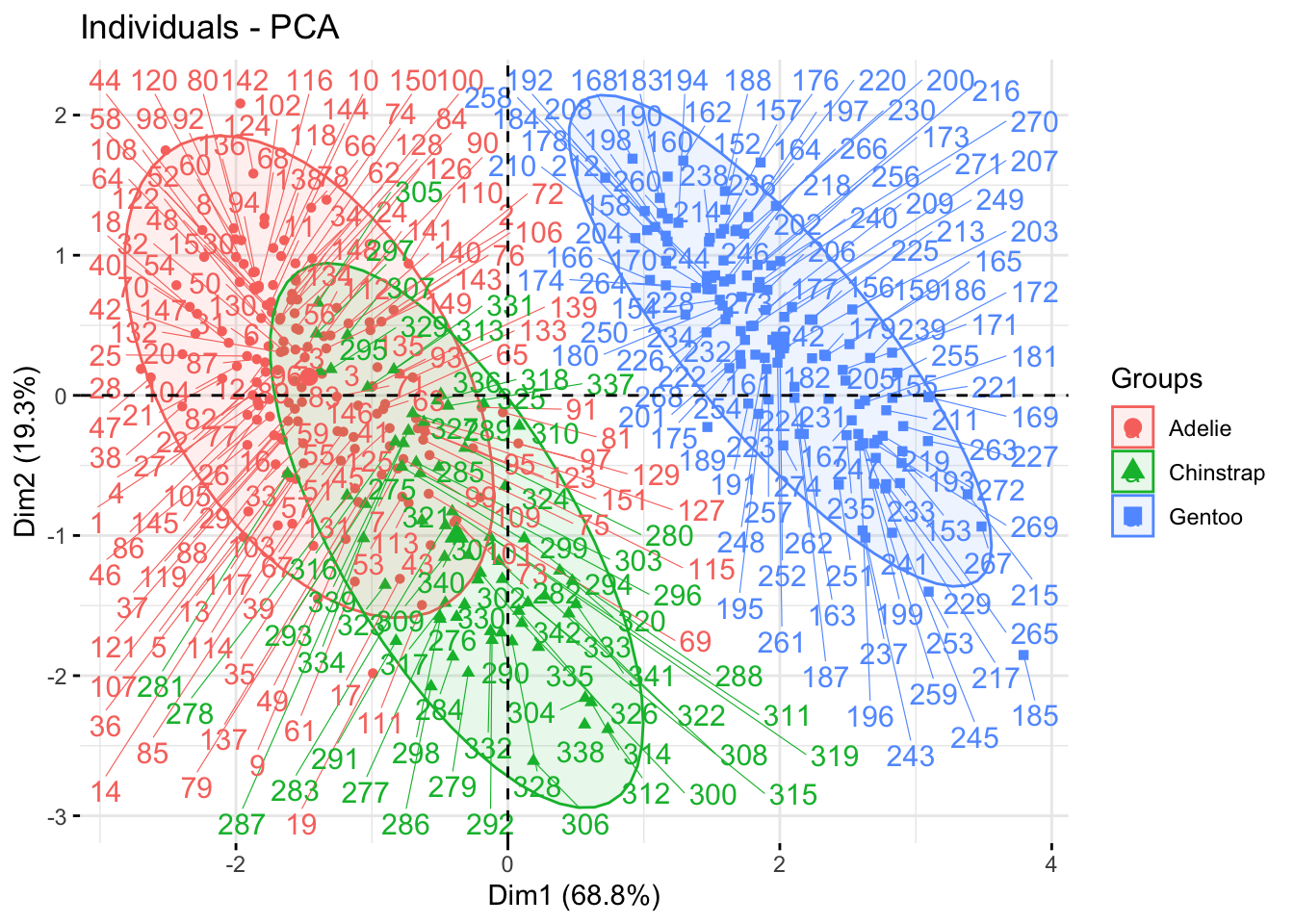
В дополнение к диаграмме рассеяния можно нарисовать график переменных функцией fviz_pca_var(). По осям \(x\) и \(y\) будут отображены первая и вторая компоненты соответственно. Как и для функции fviz_pca_ind(), можно выбрать и другие компоненты с помощью параметра axes =.
fviz_pca_var(penguins_prcomp)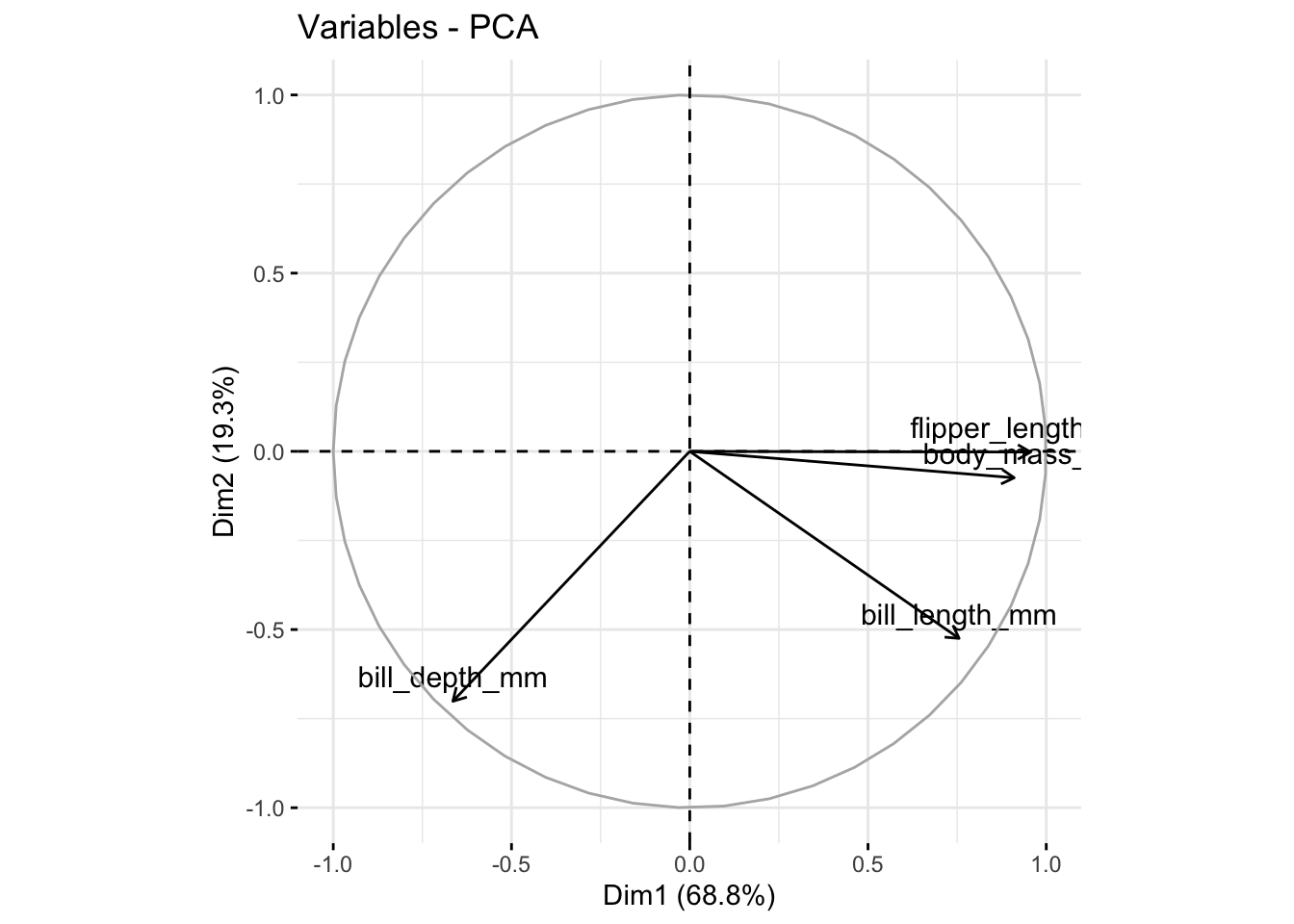
Вместо отдельных точек мы видим здесь стрелочки, которые представляют собой изначальные шкалы. Чем ближе эти стрелочки к осям \(x\) и \(y\), тем больше коэффициент корреляции между исходной шкалой и выбранной компонентой.
Если коэффициент корреляции отрицательный, то стрелочка исходной шкалы направлена в противоположную сторону от оси (влево или вниз).
Наконец, есть так называемый биплот (biplot), в котором объединены оба графика: и индивидуальные точки, и стрелочки с изначальными шкалами!
fviz_pca_biplot(penguins_prcomp,
addEllipses = TRUE,
habillage = penguins$species)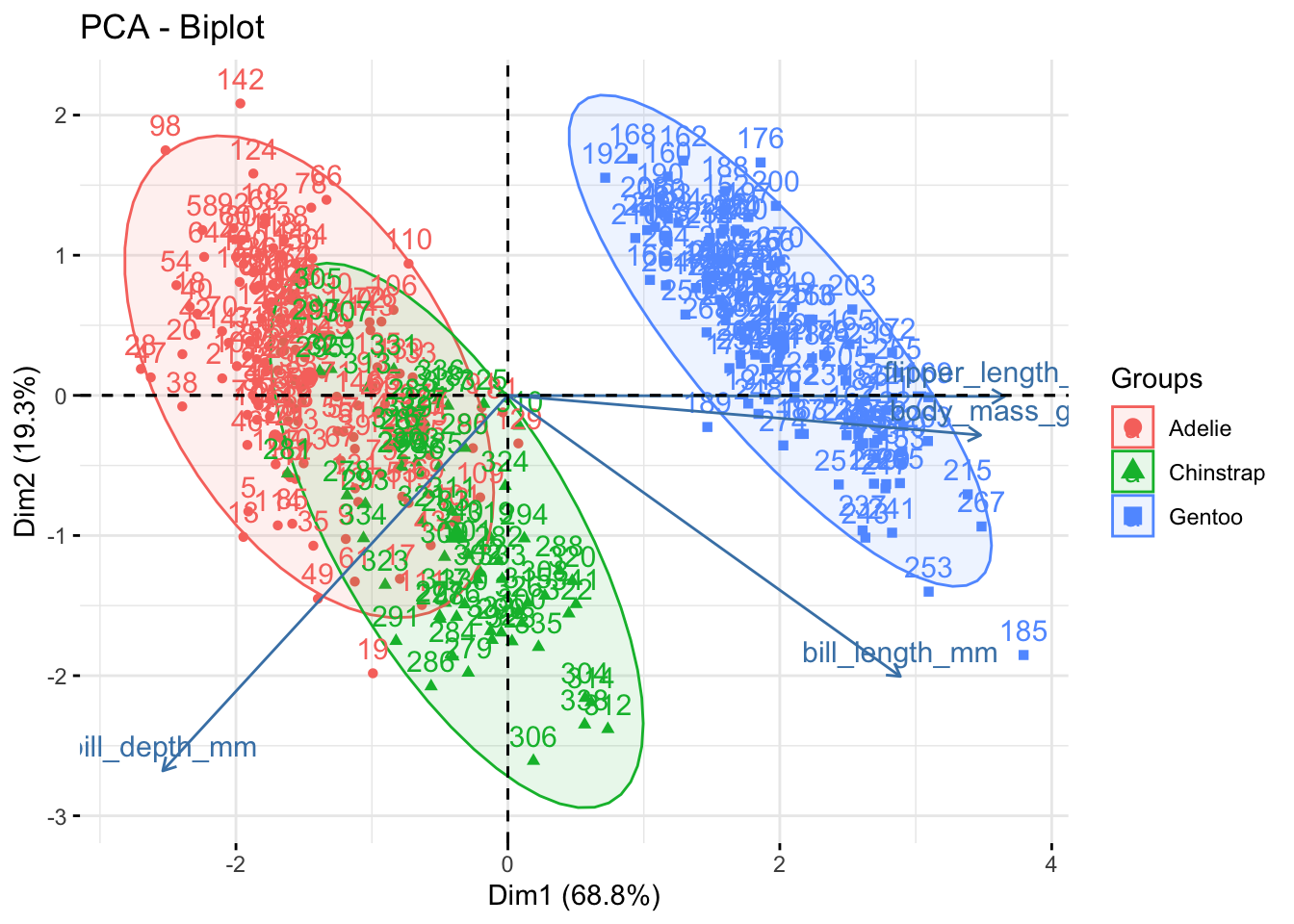
Еще один способ нарисовать биплот – с помощью пакета {ggfortify}. В этом пакете есть функция autoplot(), которая автоматически рисует что-то в зависимости от класса объекта на входе. Если это объект класса prcomp, то мы получим тот самый биплот.
library(ggfortify)
autoplot(penguins_prcomp, data = penguins, colour = "species")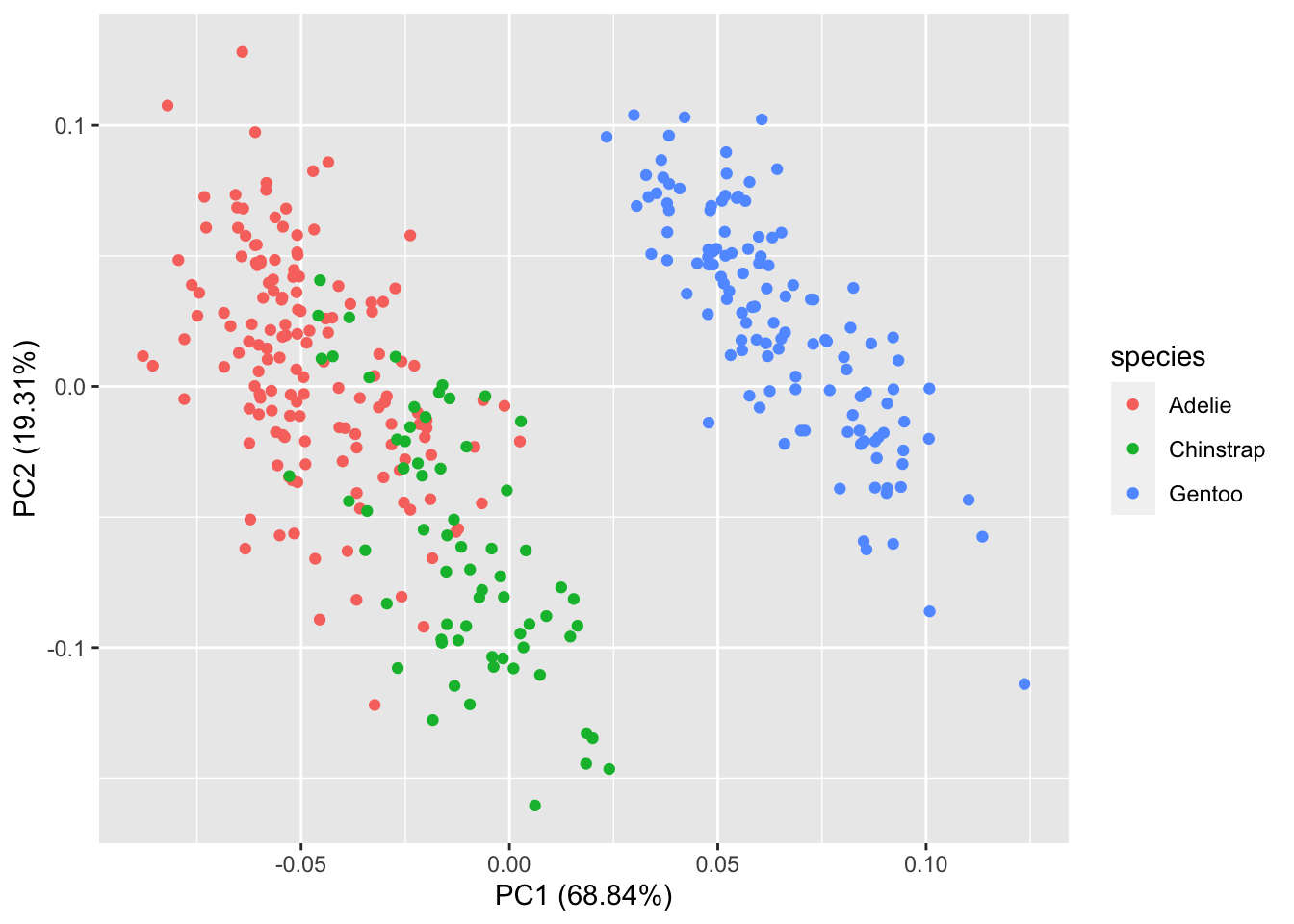
24.3 tSNE
t-Distributed Stochastic Neighbor Embedding (t-SNE) - это еще один метод снижения размерности, который используется, в основном, для визуализации многомерных данных со сложными нелинейными связями между переменными в пространстве меньшей размерности (двумерном или трехмерном).
Идея t-SNE состоит в том, чтобы расположить точки данных на такой картинке таким образом, чтобы близкие объекты оказались близко друг к другу, а далекие объекты - далеко друг от друга. Для этого используется математический подход, основанный на вероятностях и расстояниях между объектами.
Для примера возьмем знаменитый набор данных MNIST (“Modified National Institute of Standards and Technology”). MNIST – это своего рода iris или penguins в мире глубокого обучения: самый базовый учебный набор данных, на котором учатся писать искусственные нейросети. Этот набор данных очень большой, поэтому мы будем работать с его уменьшенной версией:
mnist_small <- read_csv("https://raw.githubusercontent.com/Pozdniakov/tidy_stats/master/data/mnist_small.csv")Rows: 6000 Columns: 785
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (785): label, 1x1, 1x2, 1x3, 1x4, 1x5, 1x6, 1x7, 1x8, 1x9, 1x10, 1x11, 1...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.mnist_small %>%
select(1,400:410) %>%
head()# A tibble: 6 × 12
label `15x7` `15x8` `15x9` `15x10` `15x11` `15x12` `15x13` `15x14` `15x15`
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2 0 0 22 0 0 0 0 0 0
2 8 0 0 0 0 116 254 89 54 235
3 6 0 0 0 56 252 252 252 252 252
4 1 0 0 0 0 0 0 13 200 253
5 5 0 0 0 0 32 191 233 187 145
6 3 0 27 76 44 194 204 226 253 253
# ℹ 2 more variables: `15x16` <dbl>, `15x17` <dbl>MNIST содержит большое количество написанных от руки цифр, каждый столбец – это яркость отдельного пикселя.
Особенность этого набора данных в том, что стандартными линейными методами снижения размерности такими как АГК здесь не обойтись: нужно “поймать” сложные взаимоотношения между различными пикселями, которые создают различные палки, кружочки и закорючки.
Давайте посмотрим, как справится в этой ситуации АГК:
mnist_pca <- mnist_small %>%
select(!label) %>% #удалим колонку с цифрой
select(where(function(x) !all(x == 0))) %>% #и пустые колонки удалим
prcomp(center = TRUE, scale. = TRUE)
pca_df <- mnist_pca$x[, 1:2] %>%
as_tibble() %>%
bind_cols(mnist_small$label) %>%
slice_sample(prop = .2)New names:
• `` -> `...3`names(pca_df) <- c("x", "y", "label")
pca_df %>%
ggplot() +
geom_text(aes(x = x,
y = y,
label = label,
colour = as.factor(label))) +
guides(colour = "none") +
theme_minimal()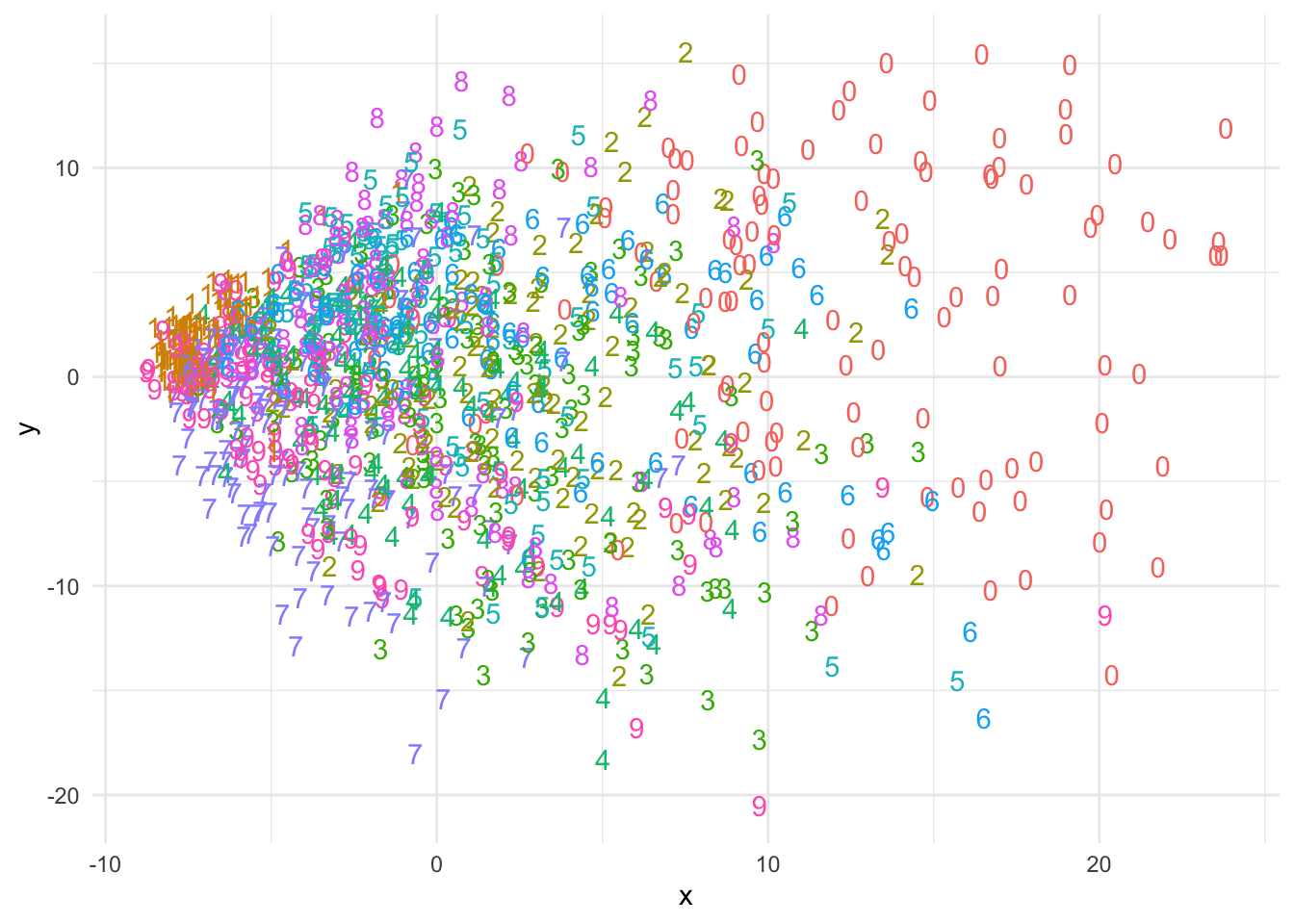
Какое-то разделение произошло, но большая часть цифр находится в общей куче.
Теперь попробуем посмотреть, что сделает с теми же данными t-SNE. Для этого воспользуемся пакетом {Rtsne}.
install.packages("Rtsne")t-SNE работает итеративно, перемещая точки на картинке, чтобы улучшить соответствие между исходными данными и их представлением на картинке. t-SNE – довольно ресурсоемкий алгоритм (особенно по сравнению с АГК), поэтому в функции Rtsne() есть множество настроек для контроля скорости ее работы. Например, можно выбрать максимальное количество итераций с помощью параметра max_iter =. Но самый главный параметр – dims =, в котором нужно задать количество измерений, которое мы хотим получить. По умолчанию dims = 2, но можно поставить, например, dims = 3, чтобы получить точки в трехмерном пространстве.
library(Rtsne)
set.seed(42)
tsne <- mnist_small %>%
select(!label) %>%
Rtsne()Теперь соединим результаты с исходными цифрами и визуализируем результаты:
tsne_df <- bind_cols(tsne$Y, mnist_small$label)New names:
• `` -> `...1`
• `` -> `...2`
• `` -> `...3`names(tsne_df) <- c("x", "y", "label")
tsne_df %>%
slice_sample(prop = .2) %>%
ggplot() +
geom_text(aes(x = x,
y = y,
label = label,
colour = as.factor(label))) +
guides(colour = "none") +
theme_minimal()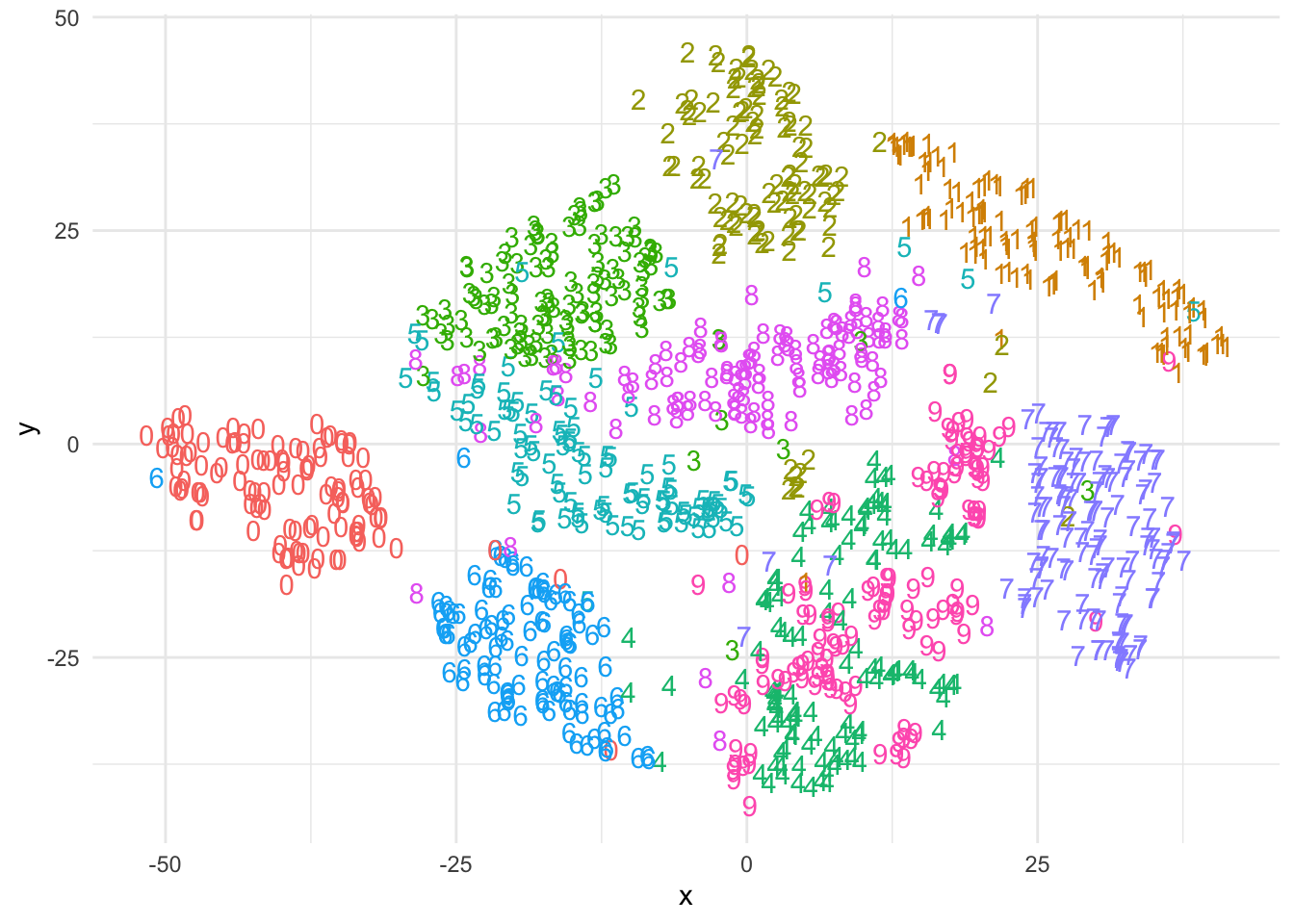
Как видите, t-SNE гораздо лучше справился с разделением цифр на группы: схожие цифры находятся рядом, непохожие – далеко. На получившемся графике заметно, что цифры 4 и 9 плохо разделись, но это довольно закономерно: эти цифры похожи по написанию.
Важно отметить, что t-SNE не сохраняет все абсолютные расстояния между объектами, поэтому важно рассматривать результат в контексте относительных расстояний. Также стоит помнить, что t-SNE не является методом для точного измерения расстояний или сравнения объектов, а скорее для визуального представления структуры данных.
24.4 Эксплораторный факторный анализ
24.5 Конфирматорный факторный анализ
24.6 Кластерный анализ
iris_3means <- kmeans(iris %>% select(!Species), centers = 3)
table(iris$Species, iris_3means$cluster)
1 2 3
setosa 50 0 0
versicolor 0 2 48
virginica 0 36 14plot(iris %>% select(!Species), col = iris$Species, pch = iris_3means$cluster)